练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，⊙O是△ABC的外接圆，AD是⊙O的直径，EA是⊙O的切线．若∠EAC=120°，则∠ABC的度数是（ ）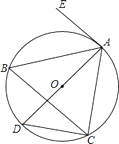

    A.80°
    B.70°
    C.60°
    D.50°

    【答案】C
    【解析】解：∵EA是⊙O的切线，AD是⊙O的直径，
    ∴∠EAD=90°，
    ∵∠EAC=120°，
    ∴∠DAC=∠EAC﹣∠EAD=30°，
    ∵AD是⊙O的直径，
    ∴∠ACD=90°，
    ∴∠ADC=180°﹣∠ACD﹣∠DAC=60°，
    ∴∠ABC=∠ADC=60°（圆周角定理），
    故选：C．
    【考点精析】关于本题考查的切线的性质定理，需要了解切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，有下列说法：①若DE∥AB，则∠DEF+∠EFB=180；

    ②能与∠DEF构成内错角的角的个数有2个；③能与∠BFE构

    成同位角的角的个数有2个；④能与∠C构成同旁内角的角的个数有4个．其中结论正确的是（ ）

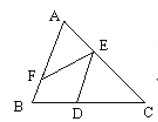
    A. ①② B. ③④ C. ①③④ D. ①②④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察图①，由点A和点B可确定　 　条直线；

    观察图②，由不在同一直线上的三点A、B和C最多能确定　 　条直线；

    （1）动手画一画图③中经过A、B、C、D四点的所有直线，最多共可作　 　条直线；

    （2）在同一平面内任三点不在同一直线的五个点最多能确定　 　条直线、n个点（n≥2）最多能确定　 　条直线．

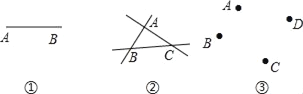
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，四边形ABCD的对角线AC、BD交于点O，若OE=OF，DF∥BE．

    （1）求证：△BOE≌△DOF；

    （2）求证：四边形DEBF是平行四边形；

    （3）若OD=OE=OF，则四边形DEBF是什么特殊的四边形，请证明．

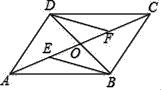
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平行四边形ABCD中，AB＝6，AD＝10，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE，垂足为G，AG＝2.5，则△CEF的周长为

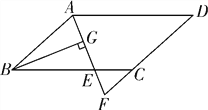
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知两直线L1：y=k1x+b1，L2：y=k2x+b2，若L1⊥L2，则有k1k2=﹣1．

    （1）应用：已知y=2x+1与y=kx﹣1垂直，求k；

    （2）直线经过A（2，3），且与y=x+3垂直，求解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，线段AB和射线BM交于点B．

    （1）利用尺规完成以下作图，并保留作图痕迹（不写作法）

    ①在射线BM上作一点C，使AC=AB；

    ②作∠ABM 的角平分线交AC于D点；

    ③在射线CM上作一点E，使CE=CD，连接DE.

    （2）在（1）所作的图形中，猜想线段BD与DE的数量关系，并证明之．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校为了满足学生借阅图书的需求,计划购买一批新书.为此,该校图书管理员对一周内本校学生从图书馆借出各类图书的数量进行了统计,结果如下图.

    请你根据统计图中的信息,解答下列问题:

    （1）补全条形图和扇形图;

    （2）该校学生最喜欢借阅哪类图书?

    (3)该校计划购买新书共600本,若按扇形统计图中的百分比来相应地确定漫画、科普、文学、其它这四类图书的购买量,求应购买这四类图书各多少本?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们知道，对任意一个正整数n都可以进行这样的分解：n=pq（p，q是正整数，且p≤q），在n的所有这种分解中，如果p，q两因数之差的绝对值最小，我们就称pq是n的最佳分解，并规定：F（n）=，例如12可以分解为112，26或34，因为12-1＞6-2＞4-3，所以34是最佳分解，所以F（n）=。

    （1）如果一个正整数是另外一个正整数b的平方，我们称正整数a是完全平方数，求证：对任意一个完全平方数m，总有F（m）=1

    （2）如果一个两位正整数t，t=10x+y　（1≤x≤y≤9，x,y为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18，那么我们就称这个数t为“吉祥数”，求所有“吉祥数”中F（t）的最大值。

    查看答案和解析>>

    同步练习册答案