
分析 由一元二次方程(2k-3)x2+4kx+2k-5=0有两个整数根,得出△=(4k)2-4(2k-3)(2k-5)≥0,根据三角形的三边关系得出0<4k+1<14,进一步联立不等式组求得解集,得出k的数值即可.
解答 解:∵一元二次方程(2k-3)x2+4kx+2k-5=0有两个整数根,
∴△=(4k)2-4(2k-3)(2k-5)
=64k-60≥0
解得k≥$\frac{15}{16}$
∵4k+1是腰长为7的等腰三角形的底边长,
∴0<4k+1<14,
∴-$\frac{1}{4}$<k<$\frac{13}{4}$,
∴$\frac{15}{16}$≤k<$\frac{13}{4}$,
∴k=1或2.
当k=2时,方程没有整数根,
∴k=1.
点评 此题考查一元二次方程的实际运用,掌握根的判别式和三角形的三边关系是解决问题的关键.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:初中数学 来源: 题型:填空题
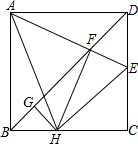 如图,在正方形ABCD中,AB=4,点E为CD上一动点,AE交BD于点F,过点F作FH⊥AE,交BC于H,过H作GH⊥BD于点G,下列结论:①AF=FH,②∠HAE=45°,③BD=$\frac{3}{2}$FG,④△CEH的周长为定值.其中正确的是①②④(写正确结论的序号).
如图,在正方形ABCD中,AB=4,点E为CD上一动点,AE交BD于点F,过点F作FH⊥AE,交BC于H,过H作GH⊥BD于点G,下列结论:①AF=FH,②∠HAE=45°,③BD=$\frac{3}{2}$FG,④△CEH的周长为定值.其中正确的是①②④(写正确结论的序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 年 | 上半年盈利 | 下半年盈利 | 算式 | 合计 |
| 第一年 | 1.2 | 0.8 | 1.2+0.8 | |
| 第二年 | -0.6 | -0.7 | (-0.6)+(-0.7) | |
| 第三年 | -0.5 | 0.5 | (-0.5)+0.5 | |
| 第四年 | 0.9 | -0.1 | 0.9+(-0.1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
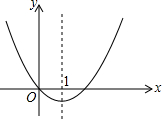 二次函数的图象如图,对称轴为x=1.若关于x的一元二次方程x2+bx-t=0(为实数)在-1<x<4的范围内有解,则t的取值范围是-1≤t<8.
二次函数的图象如图,对称轴为x=1.若关于x的一元二次方程x2+bx-t=0(为实数)在-1<x<4的范围内有解,则t的取值范围是-1≤t<8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com