
����Ŀ��2019�������г�������ˮƽ���Խ��иĸ��������ѡ��Ŀ��ѧ�����Դ������������������������ϵ��������б���ѡһ������һ��������������������Ů�����������ϣ��У���ԭ��������ʵ����������Զ�б���ѡһ��.�ֶ�������ijУ��ѡ����Ŀ������е��飬�Ե����������˷���ͳ�Ʋ�����������ͳ��ͼ��

��1����ȫ����ͳ��ͼ��
��2���������Щ��������������ƽ���֣�
��3������У��������������Գɼ��õ�����ѡ��10���μ�ȫ���˶���.������19��ѧ��������С������19��ͬѧ֮һ��С����֪���Լ���γɼ�����֪����19��ѧ���ɼ��ģ� ��������֪���Լ��ܲ��ܲμ����˶���.
A.ƽ���� B.���� C.��λ�� D.����
 �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2��bx��c(a��0)�IJ���ͼ���䶥������Ϊ(1��n)����������x���һ�������ڵ�(3��0)��(4��0)֮�䣮�����н���

��a��b��c��0����3a��b��0��
��b2��4a(c��n)��
��һԪ���η���ax2��bx��c��n��1����������ȵ�ʵ������
������ȷ���۵ĸ�����(����)
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ�˴�������У��ȥ�깺����һ��ͼ�飮���п�����ĵ��۱���ѧ��ĵ��۶�8Ԫ����1800Ԫ����Ŀ��������������l000Ԫ�������ѧ���������ͬ��
��1����ȥ�깺�����ѧ��Ϳ�����ĵ��۸��Ƕ���Ԫ��
��2������ѧУ����ƻ��ٹ�����������ѧ��Ϳ����鹲200�����ҹ�����ѧ��Ϳ�������ܷ��ò�����2088Ԫ��������ѧ��ĵ��۱�ȥ�������20%��������ĵ�����ȥ����ͬ����ÿ����1����������������1����ѧ�飬������ѧУ��������Ҫ������ٱ������飿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
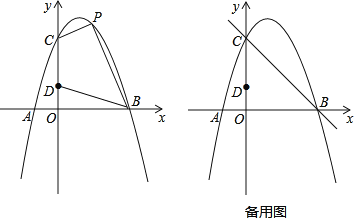
����Ŀ����ͼ���Գ���Ϊֱ��x��1�������߾���A����1��0����C��0��3�����㣬��x�����һ������ΪB����D��y���ϣ���OB��3OD
��1����������ߵı���ʽ��
��2������������ϵ�һ������P�ĺ�����Ϊt
�ٵ�0��t��3ʱ�����ı���CDBP�����S��t�ĺ�����ϵʽ�������S�����ֵ��
�ڵ�Q��ֱ��BC�ϣ�����CDΪ�ߣ���C��D��Q��PΪ������ı�����ƽ���ı��Σ���������з��������ĵ�P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾������һ�ֲ�Ʒÿ���ɱ�Ϊ40Ԫ��Ҫ����90�����������������֪�ò�Ʒ90����ÿ������ۼ۸���ʱ�䣨��x�죩�Ĺ�ϵ���±���
ʱ�䣨��x�죩 | 1��x��50 | 50��x��90 |
x+50 | 90 |
������ɺ�ͳ�Ʒ�������ԱС��90������������p��������ʱ�䣨��x�죩����һ�κ�����ϵp����2x+200����С����x����������ΪWԪ��
��1��ֱ��д��W��x֮��ĺ�����ϵʽ����ע���Ա���x��ȡֵ��Χ��
��2����С���ڼ���������������������Ƕ��٣�
��3��������ɺ�ͳ�Ʒ���ƽ��ÿ������Աÿ����������Ϊ4800��˾�ƶ����½����ƶȣ����һ������Աij�������������ƽ��ֵ���������Ա����ɻ��200Ԫ���������С��һ���ɻ�ö���Ԫ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
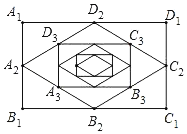
����Ŀ����ͼ��˳�����Ӿ���A1B1C1D1�ıߵ��е�õ��ı���A2B2C2D2����˳�������ı���A2B2C2D2�ıߵ��е���ı���A3B3C3D3���������˹��ɵõ��ı���AnBnnDn��������A1B1C1D1�����Ϊ8����ô�ı���AnBnnDn�����Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���D�DZ�BC�ϵĵ㣨��B��C���㲻�غϣ�������D��DE��AC��DF��AB���ֱ�AB��AC��E��F���㣬����˵����ȷ���ǣ�������

A. ��AD��BC�����ı���AEDF�Ǿ���
B. ��AD��ֱƽ��BC�����ı���AEDF�Ǿ���
C. ��BD=CD�����ı���AEDF������
D. ��ADƽ�֡�BAC�����ı���AEDF������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��[�������]
��ͼ�٣�����ABC�У���AB��6��AC��4����BC���ϵ�����AD��ȡֵ��Χ��
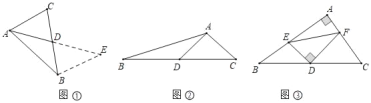
[������]
�����������������·������ӳ�AD����EʹDE��AD��������BE������ACD���ŵ�D��ʱ��װת180���õ���EBD������AB��AC��2AD��������ABE�У��������������ߵĹ�ϵ�����жϣ��ɴ˵ó�����AD��ȡֵ��Χ���� ��
[Ӧ��]
��ͼ�ڣ���ͼ������ABC�У�DΪ��BC���е㣬��֪AB��5��AC��3��AD��2����BC�ij�
[��չ]
��ͼ�ۣ�����ABC�У���A��90������D�DZ�BC���е㣬��E�ڱ�AB�ϣ�����D��DF��DE����AC�ڵ�F������EF����֪BE��4��CF��5����EF�ij�Ϊ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijũ���а���ɽ��ֲij��Ʒ������![]() ��֪�����ֵijɱ���Ϊ8Ԫ
��֪�����ֵijɱ���Ϊ8Ԫ![]() ǧ�ˣ�Ͷ���г�����ʱ�������г����飬���ָ��������۲����������ÿ������
ǧ�ˣ�Ͷ���г�����ʱ�������г����飬���ָ��������۲����������ÿ������![]() ǧ��
ǧ��![]() �����۵���
�����۵���![]() Ԫ
Ԫ![]() ǧ��
ǧ��![]() ֮��ĺ�����ϵ��ͼ��ʾ��
֮��ĺ�����ϵ��ͼ��ʾ��
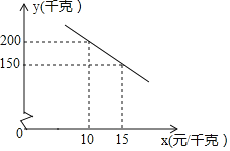
![]() ��y��x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
��y��x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
![]() ����Ʒ�����ֶ���Ϊ����ʱ��ÿ�����ۻ�õ����������������Ƕ��٣�
����Ʒ�����ֶ���Ϊ����ʱ��ÿ�����ۻ�õ����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com