
����Ŀ��ijѧУΪ�˴�������У��ȥ�깺����һ��ͼ�飮���п�����ĵ��۱���ѧ��ĵ��۶�8Ԫ����1800Ԫ����Ŀ��������������l000Ԫ�������ѧ���������ͬ��
��1����ȥ�깺�����ѧ��Ϳ�����ĵ��۸��Ƕ���Ԫ��
��2������ѧУ����ƻ��ٹ�����������ѧ��Ϳ����鹲200�����ҹ�����ѧ��Ϳ�������ܷ��ò�����2088Ԫ��������ѧ��ĵ��۱�ȥ�������20%��������ĵ�����ȥ����ͬ����ÿ����1����������������1����ѧ�飬������ѧУ��������Ҫ������ٱ������飿
���𰸡���1����ѧ��ĵ�����10Ԫ��������ĵ�����18Ԫ��(2) ����Ҫ����52�������飮
��������
��1����ȥ�깺�����ѧ��ĵ�����xԪ��������ĵ����ǣ�x+8��Ԫ�����ݡ���1800Ԫ����Ŀ��������������l000Ԫ�������ѧ���������ͬ���г����̣�
��2��������ѧУ����Ҫ����y�������飬���ݡ�������ѧ��Ϳ�������ܷ��ò�����2088Ԫ���г�����ʽ��
�⣺��1����ȥ�깺�����ѧ��ĵ�����xԪ��������ĵ����ǣ�x+8��Ԫ��
�������⣬��![]() ��
��
���x��10��
������ x��10��ԭ���̵Ľ⣮
��x��10ʱ��x+8��18��
��ȥ�깺�����ѧ��ĵ�����10Ԫ��������ĵ�����18Ԫ��
��2��������ѧУ����Ҫ����y�������飬
�������⣬��10����1+20%����200��y��y��+18y��2088
���y��52
������ѧУ��������Ҫ����52�������飮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ���ѧ���ϣ���ʦ��ʾ������һ�����⣺
��ͼ����������ABCD�У���F��AB�ϣ���E��BC�ӳ����ϡ���AF=CE������EF������D��DH��FE�ڵ�H������CH���ӳ���BD�ڵ�0����BFE=75��.��![]() ��ֵ.ijѧϰС���ͬѧ����˼�����������Լ����뷨��
��ֵ.ijѧϰС���ͬѧ����˼�����������Լ����뷨��
С�أ���ͨ���۲�Ͷ��������ֵ�H���߶�EF���е�����
С��������BFE=75����˵��ͼ�������������������
С������ͨ���۲�Ͷ���������CO��BD����
С�գ�����Ŀ�е�����������CH���ӳ���BD�ڵ�O������COƽ�֡�BCD���Ǽ�֪���������������ߺ�һ�õ�CO��BD����
С�ܣ��������е��������ߣ�ֱ�ӻ�ͨ��������ȫ�ȣ�����֤��CO��BD���Ӷ��õ���������������
��ʦ�����ӳ�DH��BC�ڵ�G����h����BFB=75��������ԭ������������ȡAD�е�M������MH���������AB��MH��ֵ����ô�������GE�ij�����.
��ش�(1)֤��FH=EH��
(2)��![]() ��ֵ��
��ֵ��
(3)��AB=4.MH=![]() ����GE�ij���Ϊ_____________.
����GE�ij���Ϊ_____________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ı���ABCD����AC��BD�ǶԽ�����E��F��G��H�ֱ����߶�BD��BC��AC��AD�ϵĵ��������ı���EFGH����״��ij���ѧ����һ����ѧ�������ͨ������ʵ����̽�������½��������д�������� ��

A. ��E��F��G��H�Ǹ����߶ε��е�ʱ���ı���EFGHΪƽ���ı���
B. ��E��F��G��H�Ǹ����߶ε��е�����AC��BDʱ���ı���EFGHΪ����
C. ��E��F��G��H�Ǹ����߶ε��е�����AB=CDʱ���ı���EFGHΪ����
D. ��E��F��G��H���Ǹ����߶ε��е�ʱ���ı���EFGH����Ϊƽ���ı���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������龳����һ��ֱ�����ǰ壨Rt��ABC��Rt��DEF����ͼ1��ʾ�ķ�ʽ�ڷţ�������ACB=90����CA=CB����FDE=90����O��AB���е㣬��D���O�غϣ�DF��AC�ڵ�M��DE��BC�ڵ�N�����ж��߶�OM��ON��������ϵ����˵�����ɣ�
̽��չʾ��С��ͬѧչʾ��������ȷ�Ľⷨ��
�⣺OM=ON��֤�����£�
����CO����CO��AB�������ߣ�
��CA=CB����CO����ACB�Ľ�ƽ���ߣ�������1��
��OM��AC��ON��BC����OM=ON��������2��
��˼������
��1������֤�������е�������1����������2���ֱ���ָ��
����1��
����2��
��2��������С�ͬ��˼����������д�����֤�����̣�
��չ���죺
��3����ͼ1�е�Rt��DEF��������BA�ķ���ƽ������ͼ2��ʾ��λ�ã�ʹ��D����BA���ӳ����ϣ�FD���ӳ�����CA���ӳ��ߴ�ֱ�ཻ�ڵ�M��BC���ӳ�����DE��ֱ�ཻ�ڵ�N������OM��ON�����ж��߶�OM��ON��������ϵ��λ�ù�ϵ����д��֤�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪![]() ���������ֱ�Ϊ
���������ֱ�Ϊ![]() ����
����![]() ����
����![]() ��ת�õ�.����
��ת�õ�.����![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() ���ϣ�Ҫʹ�ı���
���ϣ�Ҫʹ�ı���![]() Ϊƽ���ı��Σ������������ĵ�
Ϊƽ���ı��Σ������������ĵ�![]() ������Ϊ______��
������Ϊ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���֪ƽ���ı���ABCD�ĵ�A��0����2������B��3m��4m+1����m����1������C��6��2������Խ���BD����Сֵ�ǣ�������
A. 3![]() B. 2
B. 2![]() C. 5 D. 6
C. 5 D. 6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
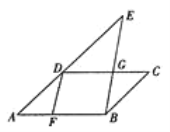
����Ŀ����ͼ��ABCD �У�G��CD��һ�㣬BG��AD�ӳ�����E��AF=CG��![]() ��
��
��1�� ��֤��DF=BG��
��2����![]() �Ķ�����
�Ķ�����
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬����OABC�У�A��10��0����C��0��4����DΪOA���е㣬PΪBC����һ�㣮����PODΪ���������Σ����������������ĵ�P������Ϊ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Сѧʱ����ѧ�����ı仯��Ϊ���Ե�ʱ�ڣ����ʱ�ں����ǵ����߱仯����һ�������ƣ�7~15���ڼ������ǻᾭ��һ�����߷�����Ѹ�ٵĽΣ����ǰ��������ν��������ٶȷ�ֵ�Σ�С��ͨ���������ġ�2016��ij�ж�ͯ���������������˽�ij����Ů��7~15������ƽ��ֵ��¼�����������������ͳ��ͼ�����ó����½��ۣ�
��10��֮ǰ��ͬ���Ů����ƽ������һ����Ը���������ƽ�����ߣ�
��10~12��֮�䣬Ů���ﵽ�����ٶȷ�ֵ�Σ����߿��ܳ���ͬ��������
��7~15���ڼ䣬������ƽ������ʼ�ո���Ů����ƽ��������
��13~15���������߳��������ٶȷ�ֵ�Σ���Ů�����߲������Ӵ�
���Ͻ�����ȷ���ǣ� ��

A. �٢� B. �ڢ� C. �ڢ� D. �ۢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com