2012年国家商务部发布了商务预报监测,猪肉价格在1~3月下跌后,已跌至肉价的最低点;而重庆市菜价,却在上演一轮5元一把的藤藤菜、12元/千克的蘑菇、30元/千克的黑豆的涨价潮,“菜价高于肉价”让普通百姓表示吃不起素.进入3月,随着本地蔬菜的大量上市,我市蔬菜价格普遍下降.以下是重庆某一超市3月份每周的蘑菇销售价格变化如下表:
| 周数x |
1 |
2 |
3 |
4 |
| 价格y(元/千克) |
12 |
6 |
4 |
3 |
已知该超市3月份每周的蘑菇销售量z
1(千克)与周数x(1≤x≤4,且x为整数)所满足的函数关系式
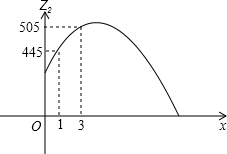
z1=-25x2+175x;进入4月份,该超市每周的蘑菇销售价格稳定在3元/千克,每周的销售量z
2(千克)与周数x(1≤x≤4,且x为整数)所满足的函数关系式为
z2=ax2+bx+400,且函数图象为下图所示:
(1)请观察题中的表格及函数图象,用你所学过的一次函数、反比例函数或二次函数的有关知识,直接写出3月份每周的销售价格y(元/千克)与周数x(1≤x≤4,且x为整数)之间的函数关系式?并直接写出4月份每周的销售量z
2(千克)与周数x(1≤x≤4,且x为整数)所满足的函数关系式?
(2)求出3月和4月分别在哪一周销售此种蘑菇的销售额最大?且最大销售额分别是多少?
(3)进入5月,重庆市由于受暴雨的影响,蔬菜运输道路堵塞,蔬菜及时供应困难,蘑菇的价格出现波动,5月的第1周蘑菇的销售价格比4月份上涨a%,销售量比4月的第4周增加0.5a%,5月份的第2周蘑菇的销售价格与5月的第1周持平,但销售量比第1周减少130千克,这样,要使5月份第2周的销售额达到4月份的最大销售额,求a的最小正整数值?(参考数据:
≈5.568, ≈5.745, ≈5.916)

 2012年国家商务部发布了商务预报监测,猪肉价格在1~3月下跌后,已跌至肉价的最低点;而重庆市菜价,却在上演一轮5元一把的藤藤菜、12元/千克的蘑菇、30元/千克的黑豆的涨价潮,“菜价高于肉价”让普通百姓表示吃不起素.进入3月,随着本地蔬菜的大量上市,我市蔬菜价格普遍下降.以下是重庆某一超市3月份每周的蘑菇销售价格变化如下表:
2012年国家商务部发布了商务预报监测,猪肉价格在1~3月下跌后,已跌至肉价的最低点;而重庆市菜价,却在上演一轮5元一把的藤藤菜、12元/千克的蘑菇、30元/千克的黑豆的涨价潮,“菜价高于肉价”让普通百姓表示吃不起素.进入3月,随着本地蔬菜的大量上市,我市蔬菜价格普遍下降.以下是重庆某一超市3月份每周的蘑菇销售价格变化如下表:

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案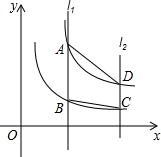 如图,平行于y轴的直线l1分别与双曲线y=
如图,平行于y轴的直线l1分别与双曲线y=