
锐角 中,
中, ,
, ,两动点
,两动点 分别在边
分别在边 上滑动,且
上滑动,且 ,以
,以 为边向下作正方形
为边向下作正方形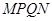 ,设其边长为
,设其边长为 ,正方形
,正方形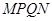 与
与 公共部分的面积为
公共部分的面积为 .
.
(1) 中边
中边 上高
上高 ;
;
(2)当 时,
时, 恰好落在边
恰好落在边 上(如图1);
上(如图1);
(3)当 在
在 外部时(如图2),求
外部时(如图2),求 关于
关于 的函数关系式(注明
的函数关系式(注明 的取值范围),并求出
的取值范围),并求出 为何值时
为何值时 最大,最大值是多少?
最大,最大值是多少? 
(1)AD=4;
(2)x=2.4;
(3)y=﹣ (x﹣3)2+6.当x=3时,y有最大值,最大值是6.
(x﹣3)2+6.当x=3时,y有最大值,最大值是6.
解析试题分析:(1)利用矩形的性质和相似三角形的性质,根据MN∥BC,得△AMN∽△ABC,求出△ABC中边BC上高AD的长度.
(2)因为正方形的位置在变化,但是△AMN∽△ABC没有改变,利用相似三角形对应边上高的比等于相似比,得出等量关系,代入解析式,
(3)用含x的式子表示矩形MEFN边长,从而求出面积的表达式.
试题解析:(1)由BC=6,S△ABC=12,得AD=4;
(2)当PQ恰好落在边BC上时,
∵MN∥BC,∴△AMN∽△ABC.
∴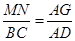 ,
,
即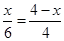 ,x=2.4;
,x=2.4;
(3)设BC分别交MP,NQ于E,F,则四边形MEFN为矩形.
设ME=NF=h,AD交MN于G(如图2)GD=NF=h,AG=4﹣h.
∵MN∥BC,
∴△AMN∽△ABC.
∴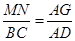 ,即
,即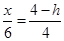 ,
,
∴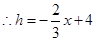 .
.
∴y=MN•NF=x(﹣ x+4)=﹣
x+4)=﹣ x2+4x(2.4<x<6),
x2+4x(2.4<x<6),
配方得:y=﹣ (x﹣3)2+6.
(x﹣3)2+6.
∴当x=3时,y有最大值,最大值是6.
考点:1.二次函数综合题2.矩形的性质.


科目:初中数学 来源: 题型:解答题
如图,已知抛物线y=2x2-2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.
(1)写出以A,B,C为顶点的三角形面积;
(2)过点E(0,6)且与x轴平行的直线l1与抛物线相交于M、N两点(点M在点N的左侧),以MN为一边,抛物线上的任一点P为另一顶点做平行四边形,当平行四边形的面积为8时,求出点P、N的坐标;
(3)过点D(m,0)(其中m>1)且与x轴垂直的直线l2上有一点Q(点Q在第一象限),使得以Q,D,B为顶点的三角形和以B,C,O为顶点的三角形相似,求线段QD的长(用含m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知在平面直角坐标系xOy中,抛物线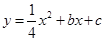 与x轴交于点A、B(点A在点B右侧),与y轴交于点C(0,-3),且OA=2OC.
与x轴交于点A、B(点A在点B右侧),与y轴交于点C(0,-3),且OA=2OC.
(1)求这条抛物线的表达式及顶点M的坐标;
(2)求 的值;
的值;
(3)如果点D在这条抛物线的对称轴上,且∠CAD=45º,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在平面直角坐标系 中,二次函数
中,二次函数 的图像与
的图像与 轴交于点A,B(点B在点A的左侧),与
轴交于点A,B(点B在点A的左侧),与 轴交于点C,过动点H(0,
轴交于点C,过动点H(0,  )作平行于
)作平行于 轴的直线,直线与二次函数
轴的直线,直线与二次函数 的图像相交于点D,E.
的图像相交于点D,E.
(1)写出点A,点B的坐标;
(2)若 ,以DE为直径作⊙Q,当⊙Q与
,以DE为直径作⊙Q,当⊙Q与 轴相切时,求
轴相切时,求 的值;
的值;
(3)直线上是否存在一点F,使得△ACF是等腰直角三角形?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连结AB、AE、BE.已知tan∠CBE= ,A(3,0),D(-1,0),E(0,3).
,A(3,0),D(-1,0),E(0,3).
(1)求抛物线的解析式及顶点B的坐标;
(2)求证:CB是△ABE外接圆的切线;
(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,直接写出点P的坐标;若不存在,请说明理由;
(4)设△AOE沿x轴正方向平移t个单位长度(0<t≤3)时,△AOE与△ABE重叠部分的面积为s,求s与t之间的函数关系式,并指出t的取值范围.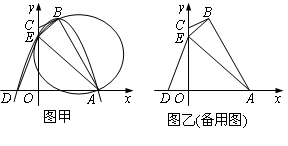
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为“梦之点”,例如点(﹣1,﹣1),(0,0),( ,
, ),…都是“梦之点”,显然,这样的“梦之点”有无数个.
),…都是“梦之点”,显然,这样的“梦之点”有无数个.
(1)若点P(2,m)是反比例函数y=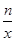 (n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;
(n为常数,n≠0)的图象上的“梦之点”,求这个反比例函数的解析式;
(2)函数y=3kx+s﹣1(k,s是常数)的图象上存在“梦之点”吗?若存在,请求出“梦之点”的坐标;若不存在,请说明理由;
(3)若二次函数y=ax2+bx+1(a,b是常数,a>0)的图象上存在两个不同的“梦之点”A(x1,x1),B(x2,x2),且满足﹣2<x1<2,|x1﹣x2|=2,令t=b2﹣2b+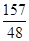 ,试求出t的取值范围.
,试求出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图1,抛物线y=ax2+bx+c(a>0)的顶点为M,直线y=m与x轴平行,且与抛物线交于点A,B,若△AMB为等腰直角三角形,我们把抛物线上A,B两点之间的部分与线段AB围成的图形称为该抛物线对应的准蝶形,线段AB称为碟宽,顶点M称为碟顶,点M到线段AB的距离称为碟高.
(1)抛物线y= x2对应的碟宽为 ;抛物线y=4x2对应的碟宽为 ;抛物线y=ax2(a>0)对应的碟宽为 ;抛物线y=a(x﹣2)2+3(a>0)对应的碟宽为 ;
x2对应的碟宽为 ;抛物线y=4x2对应的碟宽为 ;抛物线y=ax2(a>0)对应的碟宽为 ;抛物线y=a(x﹣2)2+3(a>0)对应的碟宽为 ;
(2)抛物线y=ax2﹣4ax﹣ (a>0)对应的碟宽为6,且在x轴上,求a的值;
(a>0)对应的碟宽为6,且在x轴上,求a的值;
(3)将抛物线y=anx2+bnx+cn(an>0)的对应准蝶形记为Fn(n=1,2,3…),定义F1,F2,…,Fn为相似准蝶形,相应的碟宽之比即为相似比.若Fn与Fn﹣1的相似比为 ,且Fn的碟顶是Fn﹣1的碟宽的中点,现将(2)中求得的抛物线记为y1,其对应的准蝶形记为F1.
,且Fn的碟顶是Fn﹣1的碟宽的中点,现将(2)中求得的抛物线记为y1,其对应的准蝶形记为F1.
①求抛物线y2的表达式;
②若F1的碟高为h1,F2的碟高为h2,…Fn的碟高为hn,则hn= ,Fn的碟宽有端点横坐标为 2 ;F1,F2,…,Fn的碟宽右端点是否在一条直线上?若是,直接写出该直线的表达式;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知抛物线y=x2+bx+c经过A(-1, 0)、B(4, 5)两点,过点B作BC⊥x轴,垂足为C.
(1)求抛物线的解析式;
(2)求tan∠ABO的值;
(3)点M是抛物线上的一个点,直线MN平行于y轴交直线AB于N,如果以M、N、B、C为顶点的四边形是平行四边形,求出点M的横坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com