
【题目】如图,在Rt△ABC中,AB=AC=4![]() .一动点P从点B出发,沿BC方向以每秒1个单位长度的速度匀速运动,到达点C即停止.在整个运动过程中,过点P作PD⊥BC与Rt△ABC的直角边相交于点D,延长PD至点Q,使得PD=QD,以PQ为斜边在PQ左侧作等腰直角三角形PQE.设运动时间为t秒(t>0).
.一动点P从点B出发,沿BC方向以每秒1个单位长度的速度匀速运动,到达点C即停止.在整个运动过程中,过点P作PD⊥BC与Rt△ABC的直角边相交于点D,延长PD至点Q,使得PD=QD,以PQ为斜边在PQ左侧作等腰直角三角形PQE.设运动时间为t秒(t>0).
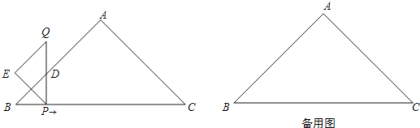
(1)在整个运动过程中,设△ABC与△PQE重叠部分的面积为S,请直接写出S与t之间的函数关系式以及相应的自变量t的取值范围;
(2)当点D在线段AB上时,连接AQ、AP,是否存在这样的t,使得△APQ成为等腰三角形?若存在,求出对应的t的值;若不存在,请说明理由;
(3)当t=4秒时,以PQ为斜边在PQ右侧作等腰直角三角形PQF,将四边形PEQF绕点P旋转,PE与线段AB相交于点M,PF与线段AC相交于点N.试判断在这一旋转过程中,四边形PMAN的面积是否发生变化?若发生变化,求出四边形PMAN的面积y与PM的长x之间的函数关系式以及相应的自变量x的取值范围;若不发生变化,求出此定值.
【答案】(1)当0<t≤4时,S=![]() t2,当4<t≤
t2,当4<t≤![]() 时,S=-
时,S=-![]() t2+8t-16,当
t2+8t-16,当![]() <t<8时,S=
<t<8时,S=![]() t2-12t+48;(2)
t2-12t+48;(2)![]() 秒或t2=(12-4
秒或t2=(12-4![]() )秒;(3)8.
)秒;(3)8.
【解析】
试题(1)当PQ过A时求出t=4,当E在AB上时求出t=![]() ,当P到C点时t=8,即分为三种情况:根据三角形面积公式求出当0<t≤4时,S=
,当P到C点时t=8,即分为三种情况:根据三角形面积公式求出当0<t≤4时,S=![]() t2,当4<t≤
t2,当4<t≤![]() 时,S=-
时,S=-![]() t2+8t-16,当
t2+8t-16,当![]() <t<8时,S=
<t<8时,S=![]() t2-12t+48;
t2-12t+48;
(2)存在,当点D在线段AB上时,求出QD=PD=t,PD=2t,过点A作AH⊥BC于点H,PH=BH-BP=4-t,在Rt△APH中求出AP=![]() ,
,
(ⅰ)若AP=PQ,则有![]() ,
,
(ⅱ)若AQ=PQ,过点Q作QG⊥AP于点G,根据△PGQ∽△AHP求出PG=![]() ,若AQ=PQ,得出
,若AQ=PQ,得出![]() .
.
(ⅲ)若AP=AQ,过点A作AT⊥PQ于点T,得出4=![]() ×2t,求出方程的解即可;
×2t,求出方程的解即可;
(3)四边形PMAN的面积不发生变化,连接AP,此时t=4秒,求出S四边形PMAN=S△APM+S△APN=S△CPN+S△APN=S△ACP=![]() ×CP×AP=8.
×CP×AP=8.
试题解析:(1)当0<t≤4时,S=![]() t2,当4<t≤
t2,当4<t≤![]() 时,S=-
时,S=-![]() t2+8t-16,当
t2+8t-16,当![]() <t<8时,S=
<t<8时,S=![]() t2-12t+48;(2)存在,理由如下:
t2-12t+48;(2)存在,理由如下:
当点D在线段AB上时,
∵AB=AC,
∴∠B=∠C=![]() (180°-∠BAC)=45°.
(180°-∠BAC)=45°.
∵PD⊥BC,
∴∠BPD=90°,
∴∠BDP=45°,
∴PD=BP=t,
∴QD=PD=t,
∴PQ=QD+PD=2t.
过点A作AH⊥BC于点H,
∵AB=AC,
∴BH=CH=![]() BC=4,AH=BH=4,
BC=4,AH=BH=4,
∴PH=BH-BP=4-t,
在Rt△APH中,AP=![]() ;
;
(ⅰ)若AP=PQ,则有![]() .
.
解得:![]() ,
,![]() (不合题意,舍去);
(不合题意,舍去);
(ⅱ)若AQ=PQ,过点Q作QG⊥AP于点G,如图(1),
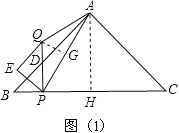
∵∠BPQ=∠BHA=90°,
∴PQ∥AH.
∴∠APQ=∠PAH.
∵QG⊥AP,
∴∠PGQ=90°,
∴∠PGQ=∠AHP=90°,
∴△PGQ∽△AHP,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
若AQ=PQ,由于QG⊥AP,则有AG=PG,即PG=![]() AP,
AP,
即![]() .
.
解得:t1=12-4![]() ,t2=12+4
,t2=12+4![]() (不合题意,舍去);
(不合题意,舍去);
(ⅲ)若AP=AQ,过点A作AT⊥PQ于点T,如图(2),
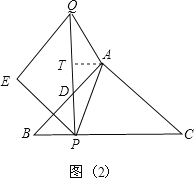
易知四边形AHPT是矩形,故PT=AH=4.
若AP=AQ,由于AT⊥PQ,则有QT=PT,即PT=![]() PQ,
PQ,
即4=![]() ×2t.解得t=4.
×2t.解得t=4.
当t=4时,A、P、Q三点共线,△APQ不存在,故t=4舍去.
综上所述,存在这样的t,使得△APQ成为等腰三角形,即![]() 秒或t2=(12-4
秒或t2=(12-4![]() )秒;
)秒;
(3)四边形PMAN的面积不发生变化.理由如下:
∵等腰直角三角形PQE,
∴∠EPQ=45°,
∵等腰直角三角形PQF,
∴∠FPQ=45°.
∴∠EPF=∠EPQ+∠FPQ=45°+45°=90°,
连接AP,如图(3),
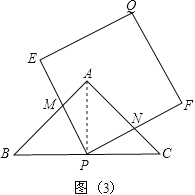
∵此时t=4秒,
∴BP=4×1=4=![]() BC,
BC,
∴点P为BC的中点.
∵△ABC是等腰直角三角形,
∴AP⊥BC,AP=![]() BC=CP=BP=4,∠BAP=∠CAP=
BC=CP=BP=4,∠BAP=∠CAP=![]() ∠BAC=45°,
∠BAC=45°,
∴∠APC=90°,∠C=45°,
∴∠C=∠BAP=45°,
∵∠APC=∠CPN+∠APN=90°,
∠EPF=∠APM+∠APN=90°,
∴∠CPN=∠APM,
∴△CPN≌△APM,
∴S△CPN=S△APM,
∴S四边形PMAN=S△APM+S△APN=S△CPN+S△APN=S△ACP=![]() ×CP×AP=
×CP×AP=![]() ×4×4=8.
×4×4=8.
∴四边形PMAN的面积不发生变化,此定值为8.
考点: 相似形综合题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() ,点
,点![]() 在
在![]() 轴上,且
轴上,且![]() .
.
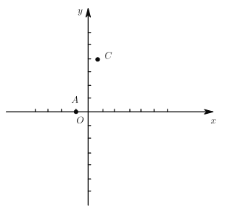
(1)求点![]() 的坐标;
的坐标;
(2)求![]() 的面积;
的面积;
(3)在![]() 轴上是否存在点
轴上是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 三点为顶点的三角形的面积为10?若存在,请直接写出点
三点为顶点的三角形的面积为10?若存在,请直接写出点![]() 的坐标.若不存在,请说明理由.
的坐标.若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°,则∠BAC的度数为( )

A. 40° B. 45° C. 60° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
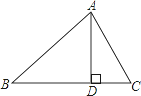
【题目】如图,△ABC中,AD⊥BC于D,下列条件:①∠B+∠DAC=90°;②∠B=∠DAC;③![]() =
=![]() ;④AB2=BDBC.其中一定能够判定△ABC是直角三角形的有( )
;④AB2=BDBC.其中一定能够判定△ABC是直角三角形的有( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形![]() 中,连接
中,连接![]() ,
,![]() 为射线
为射线![]() 上的一个动点(与点
上的一个动点(与点![]() 不重合),连接
不重合),连接![]() ,
,![]() 的垂直平分线交线段
的垂直平分线交线段![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
提出问题:当点![]() 运动时,
运动时,![]() 的度数是否发生改变?
的度数是否发生改变?
探究问题:
(1)首先考察点![]() 的两个特殊位置:
的两个特殊位置:
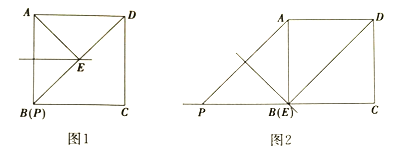
①当点![]() 与点
与点![]() 重合时,如图1所示,
重合时,如图1所示,![]() ____________
____________![]()
②当![]() 时,如图2所示,①中的结论是否发生变化?直接写出你的结论:__________;(填“变化”或“不变化”)
时,如图2所示,①中的结论是否发生变化?直接写出你的结论:__________;(填“变化”或“不变化”)
(2)然后考察点![]() 的一般位置:依题意补全图3,图4,通过观察、测量,发现:(1)中①的结论在一般情况下_________;(填“成立”或“不成立”)
的一般位置:依题意补全图3,图4,通过观察、测量,发现:(1)中①的结论在一般情况下_________;(填“成立”或“不成立”)

(3)证明猜想:若(1)中①的结论在一般情况下成立,请从图3和图4中任选一个进行证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽是4 m.按照图中所示的直角坐标系,抛物线可以用y=![]() x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为
x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为![]() m.
m.
(1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,如果点
中,如果点![]() ,点
,点![]() 为某个菱形的一组对角的顶点,且点
为某个菱形的一组对角的顶点,且点![]() 在直线
在直线![]() 上,那么称该菱形为点
上,那么称该菱形为点![]() 的“伴随菱形”,下图为点
的“伴随菱形”,下图为点![]() 的“伴随菱形”的一个示意图.
的“伴随菱形”的一个示意图.
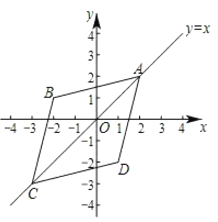
已知点![]() 的坐标为(1,1),点
的坐标为(1,1),点![]() 的坐标为
的坐标为![]() .
.
(1)点![]() 中,能够成为点
中,能够成为点![]() 的“伴随菱形”的顶点的是__________________;
的“伴随菱形”的顶点的是__________________;
(2)如果四边形![]() 是点
是点![]() 的“伴随菱形”.
的“伴随菱形”.
①当点![]() 的坐标为
的坐标为![]() 时,求四边形
时,求四边形![]() 的面积;
的面积;
②当四边形![]() 中较小内角的度数为60°时,求四边形
中较小内角的度数为60°时,求四边形![]() 的面积;
的面积;
③当四边形![]() 的面积为8,且与直线
的面积为8,且与直线![]() 有公共点时,直接写出
有公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com