
【题目】如图,已知△ABC的AC边在直线m上,∠ACB=80°,以C为圆心, ![]() BC长为半径画弧,交直线m于点D1、交BC于点E1 , 连接D1E1;又以D1为圆心,
BC长为半径画弧,交直线m于点D1、交BC于点E1 , 连接D1E1;又以D1为圆心, ![]() D1E1长为半径画弧,交直线m于点D2、交D1E1于点E2 , 连接D2E2;又以D2为圆心,
D1E1长为半径画弧,交直线m于点D2、交D1E1于点E2 , 连接D2E2;又以D2为圆心, ![]() D2E2长为半径画弧,交直线m于点D3、交D2E2于点E3 , 连接D3E3;如此依次下去,…,第n次时所得的∠EnDnDn﹣1= .
D2E2长为半径画弧,交直线m于点D3、交D2E2于点E3 , 连接D3E3;如此依次下去,…,第n次时所得的∠EnDnDn﹣1= . 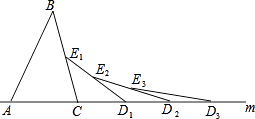
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
【题目】已知数轴上两点A,B对应的数分别为﹣4,8.
(1)如图1,如果点P和点Q分别从点A,B同时出发,沿数轴负方向运动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒6个单位.
①A,B两点之间的距离为 .
②当P,Q两点相遇时,点P在数轴上对应的数是 .
③求点P出发多少秒后,与点Q之间相距4个单位长度?
(3)如图2,如果点P从点A出发沿数轴的正方向以每秒2个单位的速度运动,点Q从点B出发沿数轴的负方向以每秒6个单位的速度运动,点M从数轴原点O出发沿数轴的正方向以每秒1个单位的速度运动,若三个点同时出发,经过多少秒后有MP=MQ?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解题过程:
已知a,b,c为△ABC的三边长,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状.
解:因为a2c2-b2c2=a4-b4, ①
所以c2(a2-b2)=( a2-b2)( a2+b2). ②
所以c2= a2+b2. ③
所以△ABC是直角三角形. ④
回答下列问题:
(1)上述解题过程,从哪一步开始出现错误?请写出该步的代码为 ;
(2)错误的原因为 ;
(3)请你将正确的解答过程写下来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个半径为18 cm的圆,从中心挖去一个正方形,当挖去的正方形的边长由小变大时,剩下部分的面积也随之发生变化.
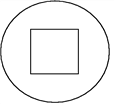
(1)若挖去的正方形边长为x(cm),剩下部分的面积为y(cm2),则y与x之间的关系式是什么?
(2)当挖去的正方形的边长由1 cm变化到9 cm时,剩下部分的面积由____变化到____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,E,G分别是BC,AC上的点,D,F是AB上的点,已知EF⊥AB,垂足为F,CD⊥AB,垂足为D,∠1=∠2, 试判断∠AGD和∠ACB是否相等,为什么?
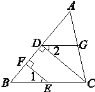
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科学技术的不断进步,我国海上能源开发和利用已达到国际领先水平.下图为我国在南海海域自主研制的海上能源开发的机器装置AB,一直升飞机在离海平面l距离为150米的空中点P处,看到该机器顶部点A处的俯角为38°,看到露出海平面的机器部分点B处的俯角为65°,求这个机器装置露出海平面部分AB的高度?(结果精确到0.1,参考数据:sin65°=0.9063,sin38°=0.6157,tan38°=0.7813,tan65°=2.1445.)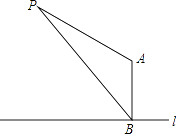
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=4cm,BC=8cm.点P从点A出发,沿AB匀速运动;点Q从点C出发,沿C→B→A→D→C的路径匀速运动.两点同时出发,在B点处首次相遇后,点P的运动速度每秒提高了3cm,并沿B→C→D→A的路径匀速运动;点Q保持速度不变,继续沿原路径匀速运动,3s后两点在长方形ABCD某一边上的E点处第二次相遇后停止运动.设点P原来的速度为xcm/s.

(1)点Q的速度为 cm/s(用含x的代数式表示);
(2)求点P原来的速度.
(3)判断E点的位置并求线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=α°,∠COD在∠AOB内部且∠COD=β°.
(1)若α,β满足|α-2β|+(β-60)2=0,则①α= ;
②试通过计算说明∠AOD与∠COB有何特殊关系;
(2)在(1)的条件下,如果作OE平分∠BOC,请求出∠AOC与∠DOE的数量关系;
(3)若α°,β°互补,作∠AOC,∠DOB的平分线OM,ON,试判断OM与ON的位置关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com