
【题目】已知点D是等边△ABC的边BC上一点,以AD为边向右作等边△ADF,DF与AC交于点N.
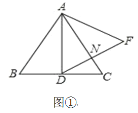
(1)如图①,当AD⊥BC时,请说明DF⊥AC的理由;
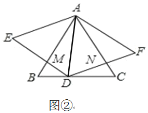
(2)如图②,当点D在BC上移动时,以AD为边再向左作等边△ADE,DE与AB交于点M,试问线段AM和AN有什么数量关系?请说明你的理由;
(3)在(2)的基础上,若等边△ABC的边长为2,直接写出DM+DN的最小值.
【答案】(1)详见解析;(2)AM=AN,理由详见解析;(3)![]()
【解析】
(1)根据等腰三角形三线合一的性质可得∠CAD=30°,再求出∠FAN=30°,然后根据等腰三角形三线合一的性质证明;
(2)根据等边三角形的每一个角都是60°可得∠ADE=∠ADF,等边三角形的三条边都相等可得AD=AF,再求出∠DAM=∠FAN,然后利用“角边角”证明△ADM和△AFN全等,根据全等三角形对应边相等即可得到AM=AN;
(3)根据垂线段最短可得DM⊥AB、DN⊥AC时,DM、DN最短,再利用△ABC的面积求出此时DM+DN等于等边△ABC的高,然后求解即可.
(1)证明:∵△ABC是等边三角形,AD⊥BC,
∴∠CAD=![]() ×60°=30°,
×60°=30°,
又∵△ADF是等边三角形,
∴∠DAF=60°,
∴∠DAN=∠FAN=30°,
∴AN⊥DF,
即DF⊥AC;
(2)AM=AN,理由如下:
∵△ADE,△ADF是等边三角形,
∴∠ADE=∠F=60°,AD=AF,
∵∠DAM+∠CAD=60°,
∠FAN+∠CAD=60°,
∴∠DAM=∠FAN,
在△ADM和△AFN中,
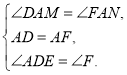
∴△ADM≌△AFN(ASA),
∴AM=AN;
(3)根据垂线段最短,DM⊥AB,DN⊥AC时,DM,DN最短,设等边△ABC的高线为h,
则![]() ,
,
![]() ,
,
∴S△ABC=![]() ACh=
ACh=![]() AC(DM+DN),
AC(DM+DN),
∴DM+DN=h,
∵等边△ABC的边长为2,
![]() .
.
∴DM+DN的最小值为![]()


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,连接BD.
(1)如图1,AE⊥BD于E.直接写出∠BAE的度数.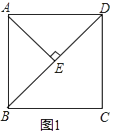
(2)如图1,在(1)的条件下,将△AEB以A旋转中心,沿逆时针方向旋转30°后得到△AB′E′,AB′与BD交于M,AE′的延长线与BD交于N.
①依题意补全图1;
②用等式表示线段BM、DN和MN之间的数量关系,并证明.
(3)如图2,E、F是边BC、CD上的点,△CEF周长是正方形ABCD周长的一半,AE、AF分别与BD交于M、N,写出判断线段BM、DN、MN之间数量关系的思路.(不必写出完整推理过程)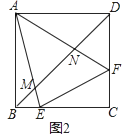
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b与反比例函数y= ![]() 交于A(﹣1,2),B(2,n),与y轴交于C点.
交于A(﹣1,2),B(2,n),与y轴交于C点.
(1)求反比例函数和一次函数解析式;
(2)如图1,若将y=kx+b向下平移,使平移后的直线与y轴交于F点,与双曲线交于D,E两点,若S△ABD=3,
求D,E的坐标.
(3)如图2,P为直线y=2上的一个动点,过点P作PQ∥y轴交直线AB于Q,交双曲线于R,若QR=2QP,求P点坐标.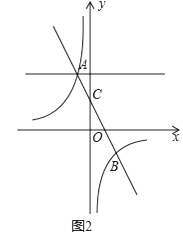
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在如图所示的平面直角坐标系中,依次连接下列各点: A(-5,0),B(1,4),C(3,3),D(1,0),E(3,-3),F(1,-4).

(2)请你在如图所示的方格纸上按照如下要求设计直角三角形:

①使它的三边中有一边边长不是有理数;
②使它的三边中有两边边长不是有理数;
③使它的三边边长都不是有理数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1,图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AB的两个端点均在小正方形的顶点上.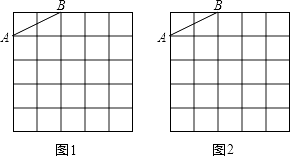
(1)如图1,在小正方形的顶点上确定一点C,连接AC、BC,使得△ABC为直角三角形,其面积为5,并直接写出△ABC的周长;
(2)如图2,在小正方形的顶点上确定一点D,连接AD、BD,使得△ABD中有一个内角为45°,且面积为3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠B=90°,AB=8cm,BC=6cm,点P从点A开始沿△ABC的边做逆时针运动,且速度为每秒1cm;点Q从点B开始沿△ABC的边做逆时针运动,且速度为每秒2cm,他们同时出发,设运动时间为t秒.

(1)出发2秒后,P,Q两点间的距离为多少cm?
(2)在运动过程中,△PQB能形成等腰三角形吗?若能,请求出几秒后第一次形成等腰三角形;若不能,则说明理由.
(3)出发几秒后,线段PQ第一次把△ABC的周长分成相等两部分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的中线,AE是BC边上的高.
(1)若∠ACB=100°,求∠CAE的度数;
(2)若S△ABC=12,CD=4,求高AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了绿化校园,计划购买一批榕树和香樟树,经市场调查,榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元.
(1)榕树和香樟树的单价各是多少?
(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵数不少于榕树的1.5倍,请你算算该校本次购买榕树和香樟树共有哪几种方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com