
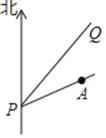
【题目】如图,台风中心位于![]() 点,并沿东北方向
点,并沿东北方向![]() 移动,已知台风移动的速度为
移动,已知台风移动的速度为![]() ,受影响区域的半径为
,受影响区域的半径为![]() ,
,![]() 市位于
市位于![]() 点的北偏东
点的北偏东![]() 方向上,距离
方向上,距离![]() 点
点![]() 处.
处.
(1)![]() 市是否受到这次台风的影响?为什么?
市是否受到这次台风的影响?为什么?
(2)若![]() 市受到台风影响,求受影响的时间有多长?
市受到台风影响,求受影响的时间有多长?
【答案】(1)见解析;(2)8h.
【解析】
(1)作AB⊥PQ于点H,在Rt△ABP中,求出BH的长与200千米相比较即可;
(2)以A为圆心,以200为半径作圆交PQ于C、D两点,求出CD的长,再根据台风的速度即可求出台风影响A市的时间.
(1)![]() 市会受到台风影响,
市会受到台风影响,
如图所示:
∵台风中心位于点P,并沿东北方向PQ移动,A市位于点P的北偏东75°方向上,
∴∠QPG=45°,∠NPA=75°,∠APG=15°,
∴∠APQ=30°,
作AB⊥PQ于点B,在Rt△ABP中,由条件知,PA=320,
得 AB=![]() PA=160<200,
PA=160<200,
∴![]() 市会受到台风影响;
市会受到台风影响;
(2)如图,以A为圆心,以200为半径作圆交PQ于C、D两点,若台风中心移动到C时,台风开始影响A市,台风中心移动到D时,台风影响结束.
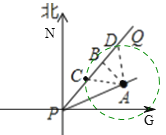
由(1)得AB=160,由条件得AC=AD=200,
由勾股定理得![]()
![]() =
=![]() =
=![]() ,
,
∴CD=2CB=240,
∴台风影响的时间t= 240÷30=8(h),
∴A市受影响时间是8h.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.

(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】乐乐家附近的商场为了吸引顾客,设立了一个可以自由转动的转盘,![]() 为转盘直径,如图所示,并规定:顾客消费50元(含50元)以上,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准9折、8折、7折区域,则顾客就可以获得相应区域的优惠.
为转盘直径,如图所示,并规定:顾客消费50元(含50元)以上,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准9折、8折、7折区域,则顾客就可以获得相应区域的优惠.

(1)某顾客在该商场消费40元,是否可以获得转动转盘的机会?
(2)某顾客在该商场正好消费66元,则他转动一次转盘,获得三种打折优惠的概率分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校初一某班学生的平均体重是45公斤.
(1)下表给出了该班6位同学的体重情况(单位:公斤),完成下表
姓 名 | 小丽 | 小华 | 小明 | 小方 | 小颖 | 小宝 |
体 重 | 37 | 50 | 40 |
| 36 | 48 |
体重与平均体重的差值 | ﹣8 | +5 |
| +2 |
|
|
(2)最重的与最轻的同学的体重相差多少?
(3)这6位同学的平均体重是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,AC=AD,增加下列条件:①AB=AE;②BC=DE;③∠C=∠D;④∠B=∠E,其中能使△ABC≌△AED的条件是______________.(填写序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
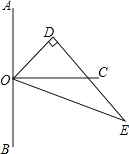
【题目】如图,点O在直线AB上,OC⊥AB,△ODE中,∠ODE=90°,∠EOD=60°,先将△ODE一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.
(1)当OD在OA与OC之间,且∠COD=20°时,则∠AOE=______;
(2)试探索:在△ODE旋转过程中,∠AOD与∠COE大小的差是否发生变化?若不变,请求出这个差值;若变化,请说明理由;
(3)在△ODE的旋转过程中,若∠AOE=7∠COD,试求∠AOE的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
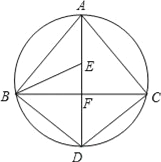
【题目】如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD,CD.
(1)求证:BD=CD;
(2)请判断B,E,C三点是否在以D为圆心,以DB为半径的圆上?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com