【题目】如图，一次函数y=ax+b与二次函数y=ax2+bx+c的大致图象是（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】
可先根据一次函数的图象判断a、b的符号，再判断二次函数图象与实际是否相符，判断正误．
A. 由一次函数y=kx+b的图象可得：a>0,b>0,此时二次函数y=ax2+bx+c的图象应该开口向上,对称轴x=
<0，错误；
B. 由一次函数y=ax+b的图象可得：a>0,此时二次函数y=ax2+bx+c的图象应该开口向上，错误；
C. 由一次函数y=ax+b的图象可得：a>0,b<0,此时二次函数y=ax2+bx+c的图象应该开口向上,对称轴x=>0，正确；
D. 由一次函数y=ax+b的图象可得：a<0,b<0,此时二次函数y=ax2+bx+c的图象应该开口向下，错误.
故答案选C.
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，已知一次函数y=kx+b的图象与反比例函数
的图象交于A，B两点，且点A的横坐标和点B的纵坐标都是﹣2，
求：（1）一次函数的解析式；
（2）△AOB的面积；
（3）直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我国古代数学著作《九章算术》中有这样一个问题：今有池方一丈，葭生其中央，出水一尺．引葭赴岸，适于岸齐，问水深、葭长各几何？”这道题的意思是说：“有一个边长为10尺的正方形水池，在水池的正中央长着一根芦苇，芦苇露出水面1尺，若将芦苇拉到水池一边的中点处，芦苇的顶端恰好到达池边的水面，问水的深度与这根芦苇的长度分别是多少？若设水的深度为x尺，则可以得到方程_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，在△ABC中，点O是AC上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于E，交∠BCA的外角平分线于F．
（1）请猜测OE与OF的大小关系，并说明你的理由；
（2）点O运动到何处时，四边形AECF是矩形？写出推理过程；
（3）点O运动到何处且△ABC满足什么条件时，四边形AECF是正方形？（写出结论即可）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知
的三个顶点坐标为
，
，
．
将绕坐标原点
旋转
，画出图形，并写出点
的对应点
的坐标________；
将绕坐标原点逆时针旋转
，直接写出点的对应点″的坐标________；
请直接写出：以、
、
为顶点的平行四边形的第四个顶点
的坐标________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知y是关于x的一次函数，下表列出了这个函数部分的对应值：
（1）求这个一次函数的表达式．
（2）求m，n的值．
（3）已知点
和点
在该一次函数图象上，设
，判断正比例函数
的图象是否有可能经过第一象限，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点是点A（3，0），其部分图象如图，则下列结论：
①2a+b=0；
②b2﹣4ac＜0；
③一元二次方程ax2+bx+c=0（a≠0）的另一个解是x=﹣1；
④点（x1，y1），（x2，y2）在抛物线上，若x1＜0＜x2，则y1＜y2．
其中正确的结论是_____（把所有正确结论的序号都填在横线上）
查看答案和解析>>
科目：初中数学 来源： 题型：
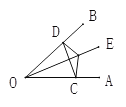
【题目】如图，点E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，垂足分别为C、D．
求证：（1）∠ECD=∠EDC；
（2）OC=OD；
（3）OE是线段CD的垂直平分线．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店购进甲、乙两种商品，已知每件甲种商品的价格比每件乙种商品的价格贵5元，用360元购买甲种商品的件数恰好与用300元购买乙种商品的件数相同．
（1）求甲、乙两种商品每件的价格各是多少元？
（2）若商店计划购买这两种商品共40件，且投入的经费不超过1150元，那么，最多可购买多少件甲种商品？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com