
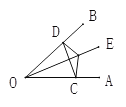
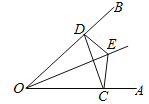
【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
求证:(1)∠ECD=∠EDC;
(2)OC=OD;
(3)OE是线段CD的垂直平分线.
【答案】见解析
【解析】
试题(1)根据角平分线性质可证ED=EC,从而可知△CDE为等腰三角形,可证∠ECD=∠EDC;
(2)由OE平分∠AOB,EC⊥OA,ED⊥OB,OE=OE,可证△OED≌△OEC,可得OC=OD;
(3)根据ED=EC,OC=OD,可证OE是线段CD的垂直平分线.
试题解析:证明:(1)∵OE平分∠AOB,EC⊥OA,ED⊥OB,∴ED=EC,即△CDE为等腰三角形,∴∠ECD=∠EDC;
(2)∵点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,∴∠DOE=∠COE,∠ODE=∠OCE=90°,OE=OE,∴△OED≌△OEC(AAS),∴OC=OD;
(3)∵OC=OD,且DE=EC,∴OE是线段CD的垂直平分线.


科目:初中数学 来源: 题型:
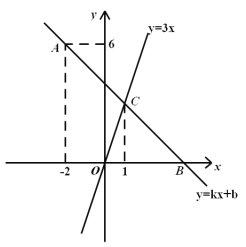
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像经过点
的图像经过点![]() ,且与
,且与![]() 轴相交于点
轴相交于点![]() ,与正比例函数
,与正比例函数![]() 的图像交于点
的图像交于点![]() ,点
,点![]() 的横坐标为
的横坐标为![]() .
.
(1)求![]()
![]() 的值;
的值;
(2)若点![]() 在
在![]() 轴上,且满足
轴上,且满足![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点C为直线AB上一点,点M、N分别是线段AC、线段BC的中点。
(1)如图,若C为线段AB上一点,AC=6,BC=4,求线段MN的长;
(2)若C为线段AB上任一点,满足AC+BC=![]() 其他条件不变,请直接写出线段MN的长(用含
其他条件不变,请直接写出线段MN的长(用含![]() 的代数式表示);
的代数式表示);
(3)若C为线段AB的延长线上一点,且满足AC-BC=![]() 其他条件不变,请直接写出线段MN的长(用含
其他条件不变,请直接写出线段MN的长(用含![]() 的代数式表示)。
的代数式表示)。
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=2x2+bx+c与直线y=﹣1只有一个公共点,且经过A(m﹣1,n)和B(m+3,n),过点A,B分别作x轴的垂线,垂足记为M,N,则四边形AMNB的周长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,AD=6,将矩形ABCD绕点B按顺时针方向旋转后得到矩形A′BC′D′.若边A′B交线段CD于H,且BH=DH,则DH的值是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请从以下两个小题中任选一个作答,若多选,则按第一题计分.
A.一个正n边形(n>4)的内角和是外角和的3倍,则n=;
B.小明站在教学楼前50米处,测得教学楼顶部的仰角为20°,测角仪的高度为1.5米,则此教学楼的高度为米.(用科学计算器计算,结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
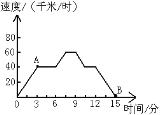
【题目】观察下图,回答问题.
(1)反映了哪两个变量之间的关系?
(2)点A,B分别表示什么?
(3)说一说速度是怎样随时间变化而变化的;
(4)你能找到一个实际情境,大致符合下图所刻画的关系吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小华和小丽两人玩游戏,她们准备了A、B两个分别被平均分成三个、四个扇形的转盘.游戏规则:小华转动A盘、小丽转动B盘.转动过程中,指针保持不动,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.两个转盘停止后指针所指区域内的数字之和小于6,小华获胜.指针所指区域内的数字之和大于6,小丽获胜. 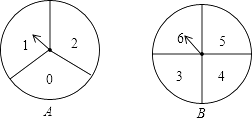
(1)用树状图或列表法求小华、小丽获胜的概率;
(2)这个游戏规则对双方公平吗?请判断并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com