
【题目】点C为直线AB上一点,点M、N分别是线段AC、线段BC的中点。
(1)如图,若C为线段AB上一点,AC=6,BC=4,求线段MN的长;
(2)若C为线段AB上任一点,满足AC+BC=![]() 其他条件不变,请直接写出线段MN的长(用含
其他条件不变,请直接写出线段MN的长(用含![]() 的代数式表示);
的代数式表示);
(3)若C为线段AB的延长线上一点,且满足AC-BC=![]() 其他条件不变,请直接写出线段MN的长(用含
其他条件不变,请直接写出线段MN的长(用含![]() 的代数式表示)。
的代数式表示)。
![]()
【答案】(1)5;(2)![]() a;(3)
a;(3)![]() b.
b.
【解析】
(1),根据线段中点的定义得到MC=![]() AC=3、NC=
AC=3、NC=![]() BC=2,然后利用线段的和差关系MN=MC+NC进行计算;
BC=2,然后利用线段的和差关系MN=MC+NC进行计算;
(2),根据线段中点的定义得到MC=![]() AC,NC=
AC,NC=![]() BC,同理利用MN=MC+NC即可得到MN的长;
BC,同理利用MN=MC+NC即可得到MN的长;
(3),首先可根据题意画出图形,然后同理利用线段中点的定义得到MC=![]() AC、NC=
AC、NC=![]() BC,进而依据MN=MC-NC求解即可.
BC,进而依据MN=MC-NC求解即可.
(1)因为点M、N分别是AC、BC的中点,
所以MC=![]() AC=
AC=![]() ×6=3,NC=
×6=3,NC=![]() BC=
BC=![]() ×4=2,
×4=2,
所以MN=MC+NC=3+2=5;
(2)因为点M、N分别是AC、BC的中点,
所以MC=![]() AC,NC=
AC,NC=![]() BC,
BC,
所以MN=MC+NC=![]() AC+
AC+![]() BC=
BC=![]() (AC+BC)=
(AC+BC)=![]() a;
a;
(3)如图所示.
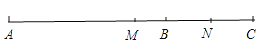
因为点M、N分别是AC、BC的中点,
所以MC=![]() AC,NC=
AC,NC=![]() BC,
BC,
所以MN=MC-NC=![]() AC-
AC-![]() BC=
BC=![]() (AC-BC)=
(AC-BC)=![]() b.
b.
故答案为:(1)5;(2)![]() a;(3)
a;(3)![]() b.
b.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-4x-m2=0
(1)求证:该方程有两个不等的实根;
(2)若该方程的两实根x1、x2满足x1+2x2=9,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
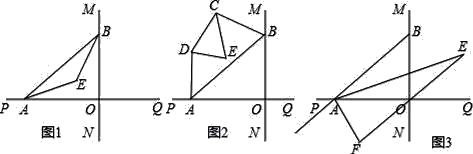
【题目】直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于三个数![]() ,用
,用![]() 表示这三个数中最大数,例如:
表示这三个数中最大数,例如:![]() ,
,![]()
解决问题:
(1)填空:![]() {
{![]() ,
,![]() ,
,![]() }= ,如果
}= ,如果![]() {
{![]() ,
,![]() ,
,![]() }=
}=![]() ,则
,则![]() 的取值范围为 ;
的取值范围为 ;
(2)如果![]() {
{![]() ,
,![]() ,
,![]() }=
}=![]() ,求
,求![]() 的值;
的值;
(3)如图,在同一坐标系中画出了三个一次函数的图象:![]() ,
,![]() 和
和![]()

请观察这三个函数的图象,
①在图中画出![]() {
{![]() ,
,![]() ,
,![]() }对应的图像(加粗);
}对应的图像(加粗);
②![]() {
{![]() ,
,![]() ,
,![]() }的最小值为 .
}的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图象中所反应的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家,其中x表示时间,y表示张强离家的距离,根据图象提供的信息,以下四个说法错误的是( )
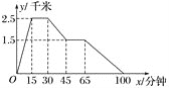
A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是![]() 千米/小时
千米/小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两种包装盒,大盒比小盒可多装20克某一物品.已知120克这一物品单独装满小盒比单独装满大盒多1盒.
(1)问小盒每个可装这一物品多少克?
(2)现有装满这一物品两种盒子共50个.设小盒有n个,所有盒子所装物品的总量为w克. ①求w关于n的函数解析式,并写出定义域;
②如果小盒所装物品总量与大盒所装物品总量相同,求所有盒子所装物品的总量.
查看答案和解析>>
科目:初中数学 来源: 题型:
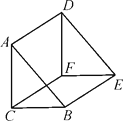
【题目】如图,三角形DEF是三角形ABC平移所得,观察图形:(1)点A的对应点是点 ,点B的对应点是点 ,点C的对应点是点 ;(2)线段AD,BE,CF叫做对应点间的连线,这三条线段之间有什么关系呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
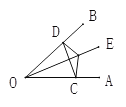
【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
求证:(1)∠ECD=∠EDC;
(2)OC=OD;
(3)OE是线段CD的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一电线杆AB的影子分别落在了地上和墙上.同一时刻,小明竖起1米高的直杆MN,量得其影长MF为0.5米,量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗? 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com