
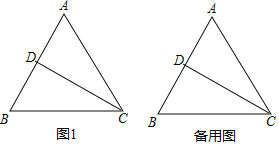
【题目】如图1,在等边三角形![]() 中,
中,![]() 为中线,点
为中线,点![]() 在线段
在线段![]() 上运动,将线段
上运动,将线段![]() 绕点
绕点![]() 顺时针旋转,使得点
顺时针旋转,使得点![]() 的对应点
的对应点![]() 落在射线
落在射线![]() 上,连接
上,连接![]() ,设
,设![]() (
(![]() 且
且![]() ).
).
(1)当![]() 时,
时,
①在图1中依题意画出图形,并求![]() (用含
(用含![]() 的式子表示);
的式子表示);
②探究线段![]() ,
,![]() ,
,![]() 之间的数量关系,并加以证明;
之间的数量关系,并加以证明;
(2)当![]() 时,直接写出线段
时,直接写出线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]()
【解析】
(1)①先根据等边三角形的性质的![]() ,进而得出
,进而得出![]() ,最后用三角形的内角和定理即可得出结论;②先判断出
,最后用三角形的内角和定理即可得出结论;②先判断出![]() ,得出
,得出![]() ,再判断出
,再判断出![]() 是底角为30度的等腰三角形,再构造出直角三角形即可得出结论;(2)同②的方法即可得出结论.
是底角为30度的等腰三角形,再构造出直角三角形即可得出结论;(2)同②的方法即可得出结论.
(1)当![]() 时,
时,
①画出的图形如图1所示,
∵![]() 为等边三角形,
为等边三角形,
∴![]() .
.
∵![]() 为等边三角形的中线
为等边三角形的中线
∴![]() 是
是![]() 的垂直平分线,
的垂直平分线,
∵![]() 为线段
为线段![]() 上的点,
上的点,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,![]() .
.
∵线段![]() 为线段
为线段![]() 绕点
绕点![]() 顺时针旋转所得,
顺时针旋转所得,
∴![]() .
.
∴![]() .
.
∴![]() ,
,
∴![]()
![]() ;
;
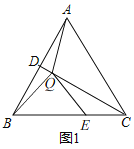
②![]() ;
;
如图2,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() ,作
,作![]() 于点
于点![]() .
.
∵![]() ,点
,点![]() 在
在![]() 上,
上,
∴![]()
![]() .
.
∵点![]() 在
在![]() 的延长线上,
的延长线上,![]() ,
,
∴![]() .
.
∴![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() 于点
于点![]() ,
,
∴![]() ,
,![]() .
.
∵在等边三角形![]() 中,
中,![]() 为中线,点
为中线,点![]() 在
在![]() 上,
上,
∴![]() ,
,
即![]() 为底角为
为底角为![]() 的等腰三角形.
的等腰三角形.
∴![]() .
.
∴![]() .
.
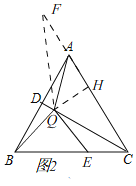
(2)如图3,当![]() 时,
时,
在![]() 上取一点
上取一点![]() 使
使![]() ,
,
∵![]() 为等边三角形,
为等边三角形,
∴![]() .
.
∵![]() 为等边三角形的中线,
为等边三角形的中线,
∵![]() 为线段
为线段![]() 上的点,
上的点,
∴![]() 是
是![]() 的垂直平分线,
的垂直平分线,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,![]() .
.
∵线段![]() 为线段
为线段![]() 绕点
绕点![]() 顺时针旋转所得,
顺时针旋转所得,
∴![]() .
.
∴![]() .
.
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() 于点
于点![]() ,
,
∴![]() ,
,![]() .
.
∵在等边三角形![]() 中,
中,![]() 为中线,点
为中线,点![]() 在
在![]() 上,
上,
∴![]() ,
,
∴![]() .
.
∴![]() .
.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】小文同学统计了某栋居民楼中全体居民每周使用手机支付的次数,并绘制了直方图.根据图中信息,下列说法:
①这栋居民楼共有居民140人
②每周使用手机支付次数为28~35次的人数最多
③有![]() 的人每周使用手机支付的次数在35~42次
的人每周使用手机支付的次数在35~42次
④每周使用手机支付不超过21次的有15人
其中正确的是( )

A.①②B.②③C.③④D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
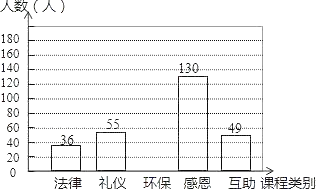
【题目】某校有学生3600人,在“文明我先行”的活动中,开设了“法律、礼仪、环保、感恩、互助”五门校本课程,规定每位学生必须且只能选一门,为了解学生的报名意向,学校随机调查了一些学生,并制成统计表和统计图:
课程类别 | 频数 | 频率 |
法律 | 36 | 0.09 |
礼仪 | 55 | 0.1375 |
环保 | m | a |
感恩 | 130 | 0.325 |
互助 | 49 | 0.1225 |
合计 | n | 1.00 |
(1)在这次调查活动中,学校采取的调查方式是 (填写“普查”或“抽样调查”)a= ,m= ,n= .
(2)请补全条形统计图,如果要画一个“校本课程报名意向扇形统计图”,那么“环保”类校本课程所对应的扇形圆心角应为 度;
(3)请估算该校3600名学生中选择“感恩”校本课程的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅游团于早上8:00从某旅行社出发,乘大巴车前往“珠海长隆”旅游,“珠海长隆”离该旅行社有100千米,导游张某因有事情,于8:30从该旅行社自驾小车以大巴1.5倍的速度追赶,追上大巴后继续前行,结果比该旅游团提前20分钟到达“珠海长隆”.
(1)大巴与小车的平均速度各是多少?
(2)导游张某追上大巴的地点到“珠海长隆”的路程有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
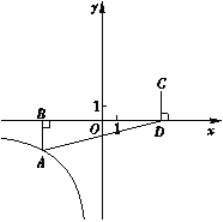
【题目】如图,在平面直角坐标系xOy中,函数![]() (
(![]() )的图象经过点
)的图象经过点![]() ,AB⊥x轴于点B,点C与点A关于原点O对称, CD⊥x轴于点D,△ABD的面积为8.
,AB⊥x轴于点B,点C与点A关于原点O对称, CD⊥x轴于点D,△ABD的面积为8.
(1)求m,n的值;
(2)若直线![]() (k≠0)经过点C,且与x轴,y轴的交点分别为点E,F,当
(k≠0)经过点C,且与x轴,y轴的交点分别为点E,F,当![]() 时,求点F的坐标.
时,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点P在∠BCA平分线CD上,且PA=PB.
(1)用尺规作出符合要求的点P(保留作图痕迹,不需要写作法);
(2)判断△ABP的形状(不需要写证明过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】研究发现:初中学生听课的注意力指标数是随着老师讲课时间的变化而变化的.讲课开始时,学生的注意力激增,中间有一段时间,学生的注意力保持平稳状态,随后开始分散.学生注意力指标数![]() 随时间
随时间![]() 变化的函数图象如图所示(
变化的函数图象如图所示(![]() 越大表示学生注意力越集中).当
越大表示学生注意力越集中).当![]() 时,图象是抛物线的一部分;当
时,图象是抛物线的一部分;当![]() 和
和![]() 时,图象是线段.根据图象回答问题:
时,图象是线段.根据图象回答问题:
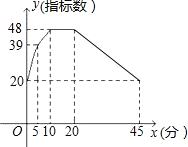
(1)课堂上,学生注意力保持平稳状态的时间段是_______.
(2)结合函数图象回答,一道几何综合题如果需要讲25分钟,老师最好在上课后大约第______分钟到第________分钟讲这道题,能使学生处于注意力比较集中的听课状态.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京世界园艺博览会(简称“世园会”)园区4月29日正式开园,门票价格如下:
票种 | 票价(元/人) | |
指定日 | 普通票 | 160 |
优惠票 | 100 | |
平日 | 普通票 | 120 |
优惠票 | 80 | |
注1:“指定日”为开园日(4月29日)、五一劳动节(5月1日)、端午节、中秋节、十一假期(含闭园日),“平日”为世园会会期除“指定日”外的其他日期;
注2:六十周岁及以上老人、十八周岁以下的学生均可购买优惠票;
注3:提前两天及以上在线上购买世园会门票,票价可打九折,但仅限于普通票.
某大家庭计划在6月1日集体入园参观游览,通过计算发现:若提前两天线上购票所需费用为996元,而入园当天购票所需费用为1080元,则该家庭中可以购买优惠票的有______人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中 过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.
(1)求证:△ABF∽△BEC;
(2)若AD=5,AB=8,sinD=![]() ,求AF的长.
,求AF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com