
【题目】已知关于x的一元二次方程(x﹣3)(x﹣2)=m2
(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求m的值及方程的另一个根.
【答案】
(1)解:∵关于x的一元二次方程(x﹣3)(x﹣2)=m2,
∴x2﹣5x+6﹣m2=0,
∴△=25﹣4(6﹣m2)=1+4m2>0,
∴对于任意实数m,方程总有两个不相等的实数根;
(2)解:若方程的一个根是1,
则(1﹣3)×(1﹣2)=m2,
2=m2,
m=± ![]() ,
,
原方程变形为x2﹣5x+4=0,
设方程的另一个根为a,
则1×a=4,
a=4,
则方程的另一个根为4.
【解析】(1)先把方程(x﹣3)(x﹣2)=m2 , 变形为x2﹣5x+6﹣m2=0,得出△=25﹣4(6﹣m2)=1+4m2>0,即可得出答案;(2)把1代入原方程,得出m,再把原方程变形为x2﹣6x+4=0,设方程的另一个根为a,根据根与系数的关系求出方程的另一个根即可.
【考点精析】本题主要考查了求根公式的相关知识点,需要掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根才能正确解答此题.


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】已知三条互相平行的直线a、b、c,请问能否作出一个等边△ABC,使其三个顶点A、B、C分别在直线a、b、c上?(用“能”或“不能”填空).若能,请说明作图方法;若不能,请简要说明理由. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y=(3-2m)x+m-1是y关于x的一次函数.
(1)若y随着x的增大而减小,求m的取值范围;
(2)若函数的图象与直线y=-3x平行,试确定该函数的表达式;
(3)若函数的图象经过点(-1,5m+2),试确定该函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等腰直角△ABC外一点,把BP绕直角顶点BB顺时针旋转90°到BP′,已知∠AP′B=135°,P′A:P′C=1:3,则PB:P′A的值为 . 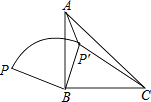
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.
(1)当D点在BC的什么位置时,DE=DF?请说明理由.
(2)DE,DF,CG的长之间存在着怎样的等量关系?并说明理由.
(3)若D在底边BC的延长线上,(2)中的结论还成立吗?若不成立,又存在怎样的关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某商场用2500元购进了A、B两种新型节能台灯共50盏,这两种台灯的进价,标价如下表所示:

(1)这两种台灯各购进多少盏?
(2)若A型台灯按标价的九折出售,B型台灯按标价的八折出售,那么这批台灯全部售完后,商场共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象经过点A(1,0).
(1)当b=2,c=﹣3时,求二次函数的解析式及二次函数最小值;
(2)二次函数的图象经过点B(m,e),C(3﹣m,e). ①求该二次函数图象的对称轴;
②若对任意实数x,函数值y都不小于 ![]() ﹣
﹣ ![]() ,求此时二次函数的解析式.
,求此时二次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,△OBC的顶点分别为O(0,0),B(3,﹣1)、C(2,1).
(1)以点O(0,0)为位似中心,按比例尺2:1在位似中心的异侧将△OBC放大为△OB′C′,放大后点B、C两点的对应点分别为B′、C′,画出△OB′C′ , 并写出点B′、C′的坐标:B′( , ),C′( , );
(2)在(1)中,若点M(x,y)为线段BC上任一点,写出变化后点M的对应点M′的坐标( , ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△OPQ是边长为 ![]() 的等边三角形,若反比例函数y=
的等边三角形,若反比例函数y= ![]() 的图像过点P. (Ⅰ)求点P的坐标和k的值;
的图像过点P. (Ⅰ)求点P的坐标和k的值;
(Ⅱ)若在这个反比例函数的图像上有两个点(x1 , y1)(x2 , y2),且x1<x2<0,请比较y1与y2的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com