
【题目】已知二次函数y=ax2+bx+c的图象经过点A(1,0).
(1)当b=2,c=﹣3时,求二次函数的解析式及二次函数最小值;
(2)二次函数的图象经过点B(m,e),C(3﹣m,e). ①求该二次函数图象的对称轴;
②若对任意实数x,函数值y都不小于 ![]() ﹣
﹣ ![]() ,求此时二次函数的解析式.
,求此时二次函数的解析式.
【答案】
(1)解:将b=2,c=﹣3代入得:y=ax2+2x﹣3.
将x=1,y=0代入,a+2﹣3=0,
∴a=1.
∴y=x2+2x﹣3=(x+1)2﹣4,
∴当x=﹣1时,y最小值为﹣4.
(2)解:①由题意可知:对称轴x= ![]() =
= ![]() .
.
②∵﹣ ![]() =
= ![]() ,
,
∴b=﹣3a,又∵a+b+c=0,
∴c=2a,
∴y=ax2﹣3ax+2a
顶点纵坐标为 ![]() =
= ![]() ,
,
∵函数值不小于 ![]() ﹣
﹣ ![]() ,
,
∴a>0,且﹣ ![]() ≥
≥ ![]() ﹣
﹣ ![]() ,
,
∴a2﹣2a+1≤0,
∴(a﹣1)2≤0,
∵(a﹣1)2≥0,
∴a﹣1=0,
∴a=1.
【解析】(1)利用待定系数法以及配方法即可解决问题.(2)①根据对称性B、C关于对称轴对称,即可解决问题.②首先求出b、c(用a表示),想办法列出不等式即可解决问题.
【考点精析】通过灵活运用二次函数的性质,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,点E、F、G、H分别在菱形ABCD的四条边上,且BE=BF=DG=DH,连接EF,FG,GH,HE得到四边形EFGH. 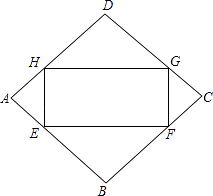
(1)求证:四边形EFGH是矩形;
(2)设AB=a,∠A=60°,当BE为何值时,矩形EFGH的面积最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆直径,D、E为圆周上两点,且AD=DE,AE与BD交于点C,则图中与∠BCE相等的角有( ) 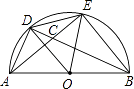
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(x﹣3)(x﹣2)=m2
(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求m的值及方程的另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列一元一次方程解应用题:
学生在素质教育基地进行社会实践活动,帮助农民伯伯采摘了黄瓜和茄子共80千克,了解到这些蔬菜的种植成本共180元,还了解到如下信息:
(1)求采摘的黄瓜和茄子各多少千克?
(2)这些采摘的黄瓜和茄子可赚多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,点D在底边BC上,添加下列条件后,仍无法判定△ABD≌△ACD的是( )

A. BD=CD B. ∠BAD=∠CAD C. ∠B=∠C D. ∠ADB=∠ADC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,![]() 可以理解为
可以理解为![]() ,它表示:数轴上表示数a的点到原点的距离,这是绝对值的几何意义。进一步地,数轴上的两个点A,B分别用数
,它表示:数轴上表示数a的点到原点的距离,这是绝对值的几何意义。进一步地,数轴上的两个点A,B分别用数![]() 表示,那么A,B两点之间的距离为
表示,那么A,B两点之间的距离为![]() ,反过来,式子
,反过来,式子![]() 的几何意义是:数轴上表示数
的几何意义是:数轴上表示数![]() 的点和表示数
的点和表示数![]() 的点之间的距离。利用此结论,
的点之间的距离。利用此结论,![]() 的意义就是数轴上表示数
的意义就是数轴上表示数![]() 的点到表示-2和表示3的点的距离之和是5,若
的点到表示-2和表示3的点的距离之和是5,若![]() 是整数,则符合
是整数,则符合![]() 的
的![]() 的个数是( )
的个数是( )
A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边三角形ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ.
(1)求证:△ABP≌△ACQ;
(2)请判断△APQ是什么三角形,试说明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com