
【题目】如图,点E、F、G、H分别在菱形ABCD的四条边上,且BE=BF=DG=DH,连接EF,FG,GH,HE得到四边形EFGH. 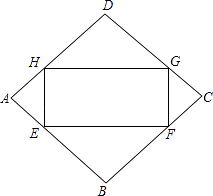
(1)求证:四边形EFGH是矩形;
(2)设AB=a,∠A=60°,当BE为何值时,矩形EFGH的面积最大?
【答案】
(1)证明:∵DG=DH,
∴∠DHG=∠DGH= ![]() ,
,
同理,∠CGF= ![]() ,
,
∴∠DGH+∠CGF= ![]() ,
,
又∵菱形ABCD中,AD∥BC,
∴∠D+∠C=180°,
∴∠DGH+∠CGF=90°,
∴∠HGF=90°,
同理,∠GHE=90°,∠EFG=90°,
∴四边形EFGH是矩形;
(2)解:AB=a,∠A=60°,则菱形ABCD的面积是: ![]() a2,
a2,
设BE=x,则AE=a﹣x,
则△AEH的面积是: ![]() ,
,
△BEF的面积是: ![]() ,
,
则矩形EFGH的面积y= ![]() a2﹣
a2﹣ ![]() ﹣
﹣ ![]() ,
,
即y=﹣ ![]() x2+
x2+ ![]() ax,
ax,
则当x= ![]() =
= ![]() 时,函数有最大值.
时,函数有最大值.
此时BE= ![]() .
.
【解析】(1)利用等腰三角形的性质:等边对等角,以及平行线的性质可以证得∠DGH+∠CGH=90°,则∠HGF=90°,根据三个角是直角的四边形是矩形,即可证得;(2)设BE的长是x,则利用x表示出矩形EFGH的面积,根据函数的性质即可求解.
【考点精析】通过灵活运用二次函数的最值和菱形的性质,掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半即可以解答此题.


科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算x[]y= ![]() (其中a,b均为非零常数),这里等式右边是通常的四则混合运算,例如:0[]2=
(其中a,b均为非零常数),这里等式右边是通常的四则混合运算,例如:0[]2= ![]() =﹣2b.
=﹣2b.
(1)已知1[]2=3,﹣1[]3=﹣2.请解答下列问题.
①求a,b的值;
②若M=(m2﹣m﹣1)[](2m﹣2m2),则称M是m的函数,当自变量m在﹣1≤m≤3的范围内取值时,函数值M为整数的个数记为k,求k的值;
(2)若x[]y=y[]x,对任意实数x,y都成立(这里x[]y和y[]x均有意义),求a与b的函数关系式?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,某客运公司的甲、乙两辆客车分别从相距380千米的A、B两地同时出发相向而行,并以各自的速度匀速行驶,两车行驶2小时时甲车先到达服务区C地,此时两车相距20千米,甲车在服务区C地休息了20分钟,然后按原速度开往B地;乙车行驶2小时15分钟时也经过C地,未停留继续开往A地.(友情提醒:画出线段图帮助分析)
(1)乙车的速度是________千米/小时,B、C两地的距离是________千米, A、C两地的距离是________千米;
(2)求甲车的速度;
(3)这一天,乙车出发多长时间,两车相距200千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知三条互相平行的直线a、b、c,请问能否作出一个等边△ABC,使其三个顶点A、B、C分别在直线a、b、c上?(用“能”或“不能”填空).若能,请说明作图方法;若不能,请简要说明理由. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。
(1)若一抛物线的顶点在原点,且经过点A(﹣2,8),求抛物线的解析式;
(2)如图,抛物线y=ax2+bx的顶点为A(﹣3,﹣3),且经过P(t,0)(t≠0),求该抛物线的解析式; 
(3)在(2)的条件下,回答下列问题(直接写出答案) ①y的最小值为;
②点P的坐标为;
③当x>﹣3时,y随x的增大而 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法: ①2a+b=0
②当﹣1≤x≤3时,y<0
③若(x1 , y1)、(x2 , y2)在函数图象上,当x1<x2时,y1<y2
④9a+3b+c=0
其中正确的是( )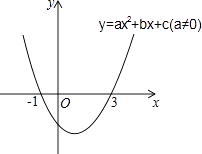
A.①②④
B.①④
C.①②③
D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A、B是数轴上的两个点,点A表示的数为13,点B表示的数为![]() ,动点P从点B出发,以每秒4个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
,动点P从点B出发,以每秒4个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
(1)点P表示的数为__________(用含t的代数式表示);
(2)点P运动多少秒时,PB=2PA?
(3)若M为BP的中点,N为PA的中点,点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请直接写出线段MN的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y=(3-2m)x+m-1是y关于x的一次函数.
(1)若y随着x的增大而减小,求m的取值范围;
(2)若函数的图象与直线y=-3x平行,试确定该函数的表达式;
(3)若函数的图象经过点(-1,5m+2),试确定该函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象经过点A(1,0).
(1)当b=2,c=﹣3时,求二次函数的解析式及二次函数最小值;
(2)二次函数的图象经过点B(m,e),C(3﹣m,e). ①求该二次函数图象的对称轴;
②若对任意实数x,函数值y都不小于 ![]() ﹣
﹣ ![]() ,求此时二次函数的解析式.
,求此时二次函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com