
【题目】对x,y定义一种新运算x[]y= ![]() (其中a,b均为非零常数),这里等式右边是通常的四则混合运算,例如:0[]2=
(其中a,b均为非零常数),这里等式右边是通常的四则混合运算,例如:0[]2= ![]() =﹣2b.
=﹣2b.
(1)已知1[]2=3,﹣1[]3=﹣2.请解答下列问题.
①求a,b的值;
②若M=(m2﹣m﹣1)[](2m﹣2m2),则称M是m的函数,当自变量m在﹣1≤m≤3的范围内取值时,函数值M为整数的个数记为k,求k的值;
(2)若x[]y=y[]x,对任意实数x,y都成立(这里x[]y和y[]x均有意义),求a与b的函数关系式?
【答案】
(1)
解:①由1[]2=3,﹣1[]3=﹣2,得
![]() ,解得
,解得 ![]() .
.
答:a的值为8,b的值为﹣1.
②把a=8,b=﹣1代入x[]y= ![]() ,得x[]y=
,得x[]y= ![]() ,
,
M=(m2﹣m﹣1)[](2m﹣2m2)=﹣2m2+2m+4=﹣2 ![]() +
+ ![]() ,
,
又∵﹣1≤m≤3,
∴当m= ![]() 时,M取最大值
时,M取最大值 ![]() ;
;
当m=﹣1时,M=0;
当m=3时,M=﹣8.
∴﹣8≤M≤ ![]() =4
=4 ![]() ,
,
∴k=8+4+1=13.
(2)
解:∵x[]y=y[]x,
∴ ![]() =
= ![]() ,
,
∴ay2﹣ax2+4by2﹣4bx2=0,
∴a(y2﹣x2)+4b(y2﹣x2)=0,
即(a+4b)(y2﹣x2)=0.
∵对任意实数x,y都成立,
∴a+4b=0,
∴a=﹣4b
【解析】(1)①结合新运算的定义,代入数据,解二元一次方程组即可得出结论;②将a、b的值代入原定义式中,用m表示出M,由二次函数的性质即可找出M的取值范围,从而得出k的值;(2)x[]y=y[]x得出关于a、b、x、y的等式,由对任意实数x,y都成立,找出恒为0的代数式a+4b=0,从而得出结论.
【考点精析】认真审题,首先需要了解有理数的四则混合运算(在没有括号的不同级运算中,先算乘方再算乘除,最后算加减).


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】已知:抛物线y=ax2﹣2(a﹣1)x+a﹣2(a>0).
(1)求证:抛物线与x轴有两个交点;
(2)设抛物线与x轴有两个交点的横坐标分别为x1 , x2 , (其中x1>x2).若y是关于a的函数,且y=ax2+x1 , 求这个函数的表达式;
(3)在(2)的条件下,结合函数的图象回答:若使y≤﹣3a2+1,则自变量a的取值范围为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=2AD, AH⊥BC于点H,E是CD的中点,连接AE、 BE、HE.
(1)求证: AE⊥BE
(2)求证:∠DEH=3 ∠ EHC

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按下列程序计算,把答案填写在表格内,然后观察有什么规律,想一想:为什么会有这个规律?
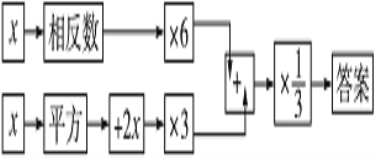
(1)填写表内空格:
输入 | -3 | -2 | -1 | 0 | … |
输出答案 | 9 |
|
|
| … |
(2)发现的规律是:输入数据x,则输出的答案是__________;
(3)为什么会有这个规律?请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
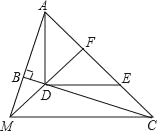
【题目】如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD、AB的延长线相交于点M,连接MC.
(1)求证:∠FMC=∠FCM;
(2)将条件中的AD⊥DE与(1)中的结论互换,其他条件不变,命题是否正确?请给出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某月的月历,用带阴影的方框任意框九个数。
(1)图中带阴影的方框中的9个数之和与方框正中心的数有什么关系?请说明你的理由?
(2)若这9个数之和是81,你能说出这9个日期吗?只要回答能或不能,且说明为什么?
(3)这9个数之和可能会是100吗?如果可能,请计算出这9个日期,如果不可能,请说明为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=5,AB的垂直平分线DE分别交AB,AC于E,D.
(1)若△BCD的周长为8,求BC的长;
(2)若BC=4,求△BCD的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线L1∥L2 , 圆O与L1和L2分别相切于点A和点B,点M和点N分别是L1和L2上的动点,MN沿L1和L2平移,圆O的半径为1,∠1=60°,当MN与圆相切时,AM的长度等于 . 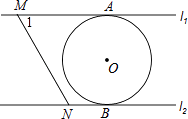
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E、F、G、H分别在菱形ABCD的四条边上,且BE=BF=DG=DH,连接EF,FG,GH,HE得到四边形EFGH. 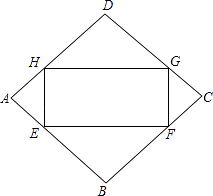
(1)求证:四边形EFGH是矩形;
(2)设AB=a,∠A=60°,当BE为何值时,矩形EFGH的面积最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com