
【题目】如图是某月的月历,用带阴影的方框任意框九个数。
(1)图中带阴影的方框中的9个数之和与方框正中心的数有什么关系?请说明你的理由?
(2)若这9个数之和是81,你能说出这9个日期吗?只要回答能或不能,且说明为什么?
(3)这9个数之和可能会是100吗?如果可能,请计算出这9个日期,如果不可能,请说明为什么?
【答案】解:(1)9个数之和是方框正中心数的9倍.
设正中心的数为x,(x-8)+(x-7)+(x-6)+(x-1)+x+(x+1)+(x+6)+(x+7)+(x+8)=9x.
∴9个数之和是方框正中心数的9倍.
(2)设正中心的数为x,依题意:9x=81,
解方程得:x=9,所以这9个日期分别为1,2,3,8,9,10,15,16,17,
所以能说出这9个日期;
(3)不可能
设中心的数为y,则列方程为9y=100,
解得y=![]() ,(不合题意,舍去)
,(不合题意,舍去)
所以不可能.
【解析】
(1)设中间的数为x,表示出其余的数,看相加的结果与中间的数的关系即可;
(2)由(1)结果得到中间的数,进而得到其他数即可;
(3)让100除以9看是不是整数,若为整数就得到9个数之和可能会是100.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙C的半径为r,P是与圆心C不重合的点,点P关于⊙C的限距点的定义如下:若P′为直线PC与⊙C的一个交点,满足r≤PP′≤2r,则称P′为点P关于⊙C的限距点,如图为点P及其关于⊙C的限距点P′的示意图. 
(1)当⊙O的半径为1时.
①分别判断点M(3,4),N( ![]() ,0),T(1,
,0),T(1, ![]() )关于⊙O的限距点是否存在?若存在,求其坐标;
)关于⊙O的限距点是否存在?若存在,求其坐标;
②点D的坐标为(2,0),DE,DF分别切⊙O于点E,点F,点P在△DEF的边上.若点P关于⊙O的限距点P′存在,求点P′的横坐标的取值范围;
(2)保持(1)中D,E,F三点不变,点P在△DEF的边上沿E→F→D→E的方向运动,⊙C的圆心C的坐标为(1,0),半径为r,请从下面两个问题中任选一个作答.
问题1 | 问题2 |
若点P关于⊙C的限距点P′存在,且P′随点P的运动所形成的路径长为πr,则r的最小值为 | 若点P关于⊙C的限距点P′不存在,则r的取值范围为 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角板按如图所示的方式摆放,其中△ABC为含有45°角的三角板,直线AD是等腰直角三角板的对称轴,且斜边上的点D为另一块三角板DMN的直角顶点,DM、DN分别交AB、AC于点E、F.则下列四个结论:①BD=AD=CD;②△AED≌△CFD;③BE+CF=EF;④S四边形AEDF=![]() BC2.其中正确结论是_____(填序号).
BC2.其中正确结论是_____(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程中变形正确的是( )
①3x+6=0变形为x+2=0;
②2x+8=5-3x变形为x=3;
③![]() +
+![]() =4去分母,得3x+2x=24;
=4去分母,得3x+2x=24;
④(x+2)-2(x-1)=0去括号,得x+2-2x-2=0.
A. ①③ B. ①②③ C. ①④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算x[]y= ![]() (其中a,b均为非零常数),这里等式右边是通常的四则混合运算,例如:0[]2=
(其中a,b均为非零常数),这里等式右边是通常的四则混合运算,例如:0[]2= ![]() =﹣2b.
=﹣2b.
(1)已知1[]2=3,﹣1[]3=﹣2.请解答下列问题.
①求a,b的值;
②若M=(m2﹣m﹣1)[](2m﹣2m2),则称M是m的函数,当自变量m在﹣1≤m≤3的范围内取值时,函数值M为整数的个数记为k,求k的值;
(2)若x[]y=y[]x,对任意实数x,y都成立(这里x[]y和y[]x均有意义),求a与b的函数关系式?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2﹣2x+3 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PMNQ的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=2 ![]() DQ,求点F的坐标.
DQ,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c,自变量x与函数y的对应值如表:
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | … |
y | … | 4 | 0 | ﹣2 | ﹣2 | 0 | 4 | … |
下列说法正确的是( )
A.抛物线的开口向下
B.当x>﹣3时,y随x的增大而增大
C.二次函数的最小值是﹣2
D.抛物线的对称轴是x=﹣ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、C、N三点在同一直线上,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,若△MNC≌△ABC,则∠BCM:∠BCN=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法: ①2a+b=0
②当﹣1≤x≤3时,y<0
③若(x1 , y1)、(x2 , y2)在函数图象上,当x1<x2时,y1<y2
④9a+3b+c=0
其中正确的是( )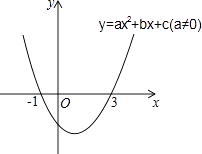
A.①②④
B.①④
C.①②③
D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com