
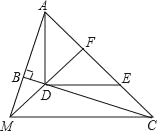
【题目】如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD、AB的延长线相交于点M,连接MC.
(1)求证:∠FMC=∠FCM;
(2)将条件中的AD⊥DE与(1)中的结论互换,其他条件不变,命题是否正确?请给出理由.
【答案】(1)证明见解析;(2)(2)正确.理由见解析.
【解析】
(1)根据等腰直角三角形的性质,得出DF⊥AE,DF=AF=EF,再证明△DFC≌△AFM,得出FC=FM;
(2)根据等腰三角形的判定,得出FM=FC,再根据等腰三角形的性质,可得MF⊥AC,进而证得△AMF≌△DCF(ASA),最后由全等三角形的性质和直角的关系可证.
(1)证明:∵AD=DE,点F是AE的中点,
∴MF⊥AC,∴∠AMF+∠MAF=90°.
∵∠ABC=90°,∴∠ACB+∠MAF=90°,
∴∠AMF=∠ACB.
∵AD⊥DE,AD=DE,
∴△ADE为等腰直角三角形,∠DAF=45°.
又∵MF⊥AC,∴∠DFA=90°,
∴∠ADF=180°-∠DFA-∠DAF=45°,
∴∠ADF=∠DAF,∴FA=FD.
在△FAM和△FDC中,
∠AMF=∠DCF,∠AFM=∠DFC,FA=FD,
∴△FAM≌△FDC(AAS),
∴FM=FC,∴∠FMC=∠FCM.
(2)解:正确.理由如下:∵∠FMC=∠FCM,∴FM=FC.
∵AD=DE,点F是AE的中点,∴MF⊥AC,
∴∠AFM=∠DFC=90°,∠AMF+∠MAC=90°.
又∵∠MAC+∠DCF=90°,
∴∠AMF=∠DCF.
在△AMF和△DCF中,
∠AMF=∠DCF,FM=FC,∠AFM=∠DFC,
∴△AMF≌△DCF(ASA),
∴AF=DF.
又∵∠AFD=90°,∴∠DAF=∠ADF=45°.
又∵AD=DE,∴∠DEA=∠DAF=45°,
∴∠ADE=180°-∠DAF-∠DEA=90°,
∴AD⊥DE.


科目:初中数学 来源: 题型:
【题目】出租车司机小李某天下午的营运全是在东西走向的人民大街上进行的.如果规定向东为正,向西为负,他这天下午行车里程(单位:千米)如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 人民大街总长不小于________千米;
人民大街总长不小于________千米;
![]() 将最后一名乘客送往目的地时,小李距离下午出车时的出发点多远?
将最后一名乘客送往目的地时,小李距离下午出车时的出发点多远?
![]() 若出租车耗油量为每千米
若出租车耗油量为每千米![]() 升,这天下午小李共耗油多少升?
升,这天下午小李共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b>0;②abc<0;③b2﹣4ac>0;④a+b+c<0;⑤4a﹣2b+c<0,其中正确的个数是( ) 
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D在BC边上,点E在AC的延长线上,DE=DA.
(1)求证:∠BAD=∠EDC;
(2)作出点E关于直线BC的对称点M,连接DM、AM,猜想DM与AM的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算x[]y= ![]() (其中a,b均为非零常数),这里等式右边是通常的四则混合运算,例如:0[]2=
(其中a,b均为非零常数),这里等式右边是通常的四则混合运算,例如:0[]2= ![]() =﹣2b.
=﹣2b.
(1)已知1[]2=3,﹣1[]3=﹣2.请解答下列问题.
①求a,b的值;
②若M=(m2﹣m﹣1)[](2m﹣2m2),则称M是m的函数,当自变量m在﹣1≤m≤3的范围内取值时,函数值M为整数的个数记为k,求k的值;
(2)若x[]y=y[]x,对任意实数x,y都成立(这里x[]y和y[]x均有意义),求a与b的函数关系式?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两果园分别产有苹果10吨和40吨,现全部运送到A、B两地销售,根据市场调研,A、B两地分别需要苹果15吨和35吨;已知从甲、乙地到A、B地的运价如表,由以上信息,解决下列问题:
到A地运价 | 到B地运价 | |
甲果园 | 150元∕吨 | 120元∕吨 |
乙果园 | 100元∕吨 | 90元∕吨 |
(1)若从乙果园运到A地的苹果为![]() 吨,则从甲果园运到B地的苹果为 吨;从甲果园将苹果运往A地的运输费用为 元(用含
吨,则从甲果园运到B地的苹果为 吨;从甲果园将苹果运往A地的运输费用为 元(用含![]() 的代数式表示);
的代数式表示);
(2)若运往A地的运输费用比运往B地的运输费用少1150元,用你所学的知识来说明是怎样安排运输方案的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点).有下列结论: ①当x=3时,y=0;
②3a+b>0;
③﹣1≤a≤﹣ ![]() ;
;
④ ![]() ≤n≤4.
≤n≤4.
其中正确的有( )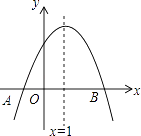
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。
(1)若一抛物线的顶点在原点,且经过点A(﹣2,8),求抛物线的解析式;
(2)如图,抛物线y=ax2+bx的顶点为A(﹣3,﹣3),且经过P(t,0)(t≠0),求该抛物线的解析式; 
(3)在(2)的条件下,回答下列问题(直接写出答案) ①y的最小值为;
②点P的坐标为;
③当x>﹣3时,y随x的增大而 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com