
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象相较于A(2,3),B(﹣3,n)两点.
的图象相较于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b>![]() 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.
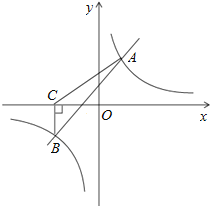
【答案】(1)反比例函数的解析式为:y=![]() ,一次函数的解析式为:y=x+1;
,一次函数的解析式为:y=x+1;
(2)﹣3<x<0或x>2;
(3)5.
【解析】
(1)根据点A位于反比例函数的图象上,利用待定系数法求出反比例函数解析式,将点B坐标代入反比例函数解析式,求出n的值,进而求出一次函数解析式
(2)根据点A和点B的坐标及图象特点,即可求出反比例函数值大于一次函数值时x的取值范围
(3)由点A和点B的坐标求得三角形以BC 为底的高是10,从而求得三角形ABC 的面积
解:(1)∵点A(2,3)在y=![]() 的图象上,∴m=6,
的图象上,∴m=6,
∴反比例函数的解析式为:y=![]() ,
,
∴n=![]() =﹣2,
=﹣2,
∵A(2,3),B(﹣3,﹣2)两点在y=kx+b上,
∴ ,
,
解得:![]() ,
,
∴一次函数的解析式为:y=x+1;
(2)由图象可知﹣3<x<0或x>2;
(3)以BC为底,则BC边上的高为3+2=5,
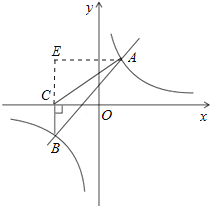
∴S△ABC=![]() ×2×5=5.
×2×5=5.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:
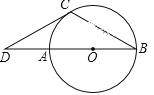
【题目】已知:如图,AB是⊙O的直径,BC是弦,∠B=30°,延长BA到D,使∠BDC=30°.
(1)求证:DC是⊙O的切线;
(2)若AB=2,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE.
(1)求证:AD=DE;
(2)求∠DCE的度数;
(3)若BD=1,求AD,CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
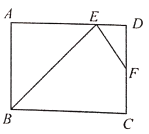
【题目】如图,矩形ABCD中,∠ABC的平分线交AD边于点E,点F是CD的中点,连接EF,若AB=8,且EF平分∠BED,则AD的长为_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC
其中正确的是( )

A. ①②③④ B. ②③ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为⊙O内接等边三角形,将△ABC绕圆心O旋转30°到△DEF处,连接AD、AE,则∠EAD的度数为( )
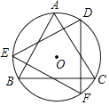
A.150°B.135°C.120°D.105°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.

(1)证明:DF是⊙O的切线;
(2)若AC=3AE,FC=6,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
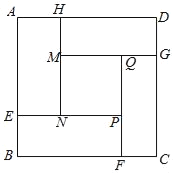
【题目】创客联盟的队员想用3D打印完成一幅边长为6米的正方形作品ABCD,设计图案如图所示(四周阴影是四个全等的矩形,用材料甲打印;中心区是正方形MNPQ,用材料乙打印).在打印厚度保持相同的情况下,两种材料的消耗成本如下表:
材料 | 甲 | 乙 |
价格(元/米2) | 80 | 50 |
设矩形的较短边AH的长为x米,打印材料的总费用为y元.
(1)MQ的长为 米(用含x的代数式表示);
(2)求y关于x的函数解析式;
(3)当中心区的边长不小于2米时,预备材料的购买资金2800元够用吗?请利用函数的增减性来说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]()
(1)将其化成![]() 的形式_______________;
的形式_______________;
(2)顶点坐标_________对称轴方程_______________;
(3)用五点法画出二次函数的图象;
(4) 当![]() 时,写出
时,写出![]() 的取值范围
的取值范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com