
����Ŀ������ʵ�����У����ǻῴ�����ࡰ�����ľ��Σ������ǵĿα����桢A4�Ĵ�ӡֽ�ȣ���ʵ��Щ���εij����֮�ȶ�Ϊ![]() ��1�����Dz����Ͱ������ľ��γ�Ϊ�������Ρ����ڡ������Ρ�ABCD�У�PΪDC����һ���㣬��CP=BC����ͼ��ʾ��
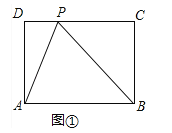
��1�����Dz����Ͱ������ľ��γ�Ϊ�������Ρ����ڡ������Ρ�ABCD�У�PΪDC����һ���㣬��CP=BC����ͼ��ʾ��

��1����ͼ������֤��BA=BP��
��2����ͼ������Q��DC�ϣ���DQ=CP����GΪBC����һ���㣬����AGQ���ܳ���Сʱ����![]() ��ֵ��
��ֵ��
��3����ͼ������֪AD=1���ڣ�2���������£�����AG���ӳ���DC���ӳ����ڵ�F������BF��TΪBF���е㣬M��N�ֱ�Ϊ�߶�PF��AB�ϵĶ��㣬��ʼ�ձ���PM=BN����֤������MNT�����SΪ��ֵ������������ֵ��
���𰸡���1��֤������������2��![]() ����3����ֵΪ��
����3����ֵΪ��![]() ��
��
��������
�����������1����ͼ���У���AD=BC=a����AB=CD=![]() a��ͨ������ó�AB=BP=
a��ͨ������ó�AB=BP=![]() a���ɴ˼���֤����
a���ɴ˼���֤����
��2����ͼ���У���Q����BC�ĶԳƵ�Q�䣬����AQ�佻BC��G����ʱ��AQG���ܳ���С����AD=BC=QD=a����AB=CD=![]() a���ɵ�CQ=CQ��=
a���ɵ�CQ=CQ��=![]() a��a����CQ����AB���Ƴ�
a��a����CQ����AB���Ƴ�![]() ��ֵ��
��ֵ��
��3����ͼ���У���TH��AB��NM��H����BC��K����S��MNT=![]() THCK+
THCK+![]() THBK=
THBK=![]() HT��KC+KB��=
HT��KC+KB��=![]() HTBC=
HTBC=![]() HT���������ε���λ�߶������HT���ɽ�����⣻
HT���������ε���λ�߶������HT���ɽ�����⣻
�����������1��֤������ͼ���У���AD=BC=a����AB=CD=![]() a��
a��
���ı���ABCD�Ǿ��Σ����C=90�㣬��PC=AD=BC=a����PB=![]() =
=![]() a����BA=BP��
a����BA=BP��
��2���⣺��ͼ���У���Q����BC�ĶԳƵ�Q�䣬����AQ�佻BC��G����ʱ��AQG���ܳ���С��

��AD=BC=QD=a����AB=CD=![]() a����CQ=CQ��=
a����CQ=CQ��=![]() a��a����CQ����AB����
a��a����CQ����AB����![]() =
=![]() =
=![]() =
=![]() ��
��
��3��֤������ͼ���У���TH��AB��NM��H����BC��K��

�ɣ�2����֪��AD=BC=1��AB=CD=![]() ��DP=CF=
��DP=CF=![]() ��1����S��MNT=
��1����S��MNT=![]() THCK+
THCK+![]() THBK=
THBK=![]() HT��KC+KB��=
HT��KC+KB��=![]() HTBC=
HTBC=![]() HT����TH��AB��FM��TF=TB����HM=HN����HT=
HT����TH��AB��FM��TF=TB����HM=HN����HT=![]() ��FM+BN������BN=PM����HT=
��FM+BN������BN=PM����HT=![]() ��FM+PM��=
��FM+PM��=![]() PF=
PF=![]() ��1+
��1+![]() ��1��=
��1��=![]() ����S��MNT=
����S��MNT=![]() HT=
HT=![]() =��ֵ��
=��ֵ��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���е㣮
���е㣮

��1����֤��![]() ��
��![]() ��
��
��2������![]() ����
����![]() ����
����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O����ABC�����Բ��BCΪ��O��ֱ������EΪ��ABC�����ģ�����AE���ӳ�����O��D�㣬����BD���ӳ���F��ʹ��BD=DF������CF��BE��
��1����֤��DB=DE��
��2����֤��ֱ��CFΪ��O�����ߣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������ε�����������ڵ��ڽ�֮��Ϊ1��3����ô�������εı���Ϊ�� ��
A.8B.9C.10D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽����о��꼶840��ѧ����������������г�ȡ100��ѧ�������ؽ��з���������������У�������ָ��������
A.840��ѧ��B.����ȡ��100��ѧ��
C.840��ѧ��������D.����ȡ��100��ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���![]() �У�
��![]() ��
��![]() Ϊ
Ϊ![]() �ߵ��е㣮��
�ߵ��е㣮��![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת
˳ʱ����ת![]() ����
����![]() �Ķ�Ӧ��Ϊ
�Ķ�Ӧ��Ϊ![]() ����
����![]() �Ķ�Ӧ��Ϊ
�Ķ�Ӧ��Ϊ![]() ������
������![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ���ڵ�
���ڵ�![]() .�������н��ۣ���
.�������н��ۣ���![]() ����
����![]() ����
����![]() ������
������![]() Ϊ
Ϊ![]() ������.
������.
������ȷ���۵ĸ���Ϊ�� ��

A��1�� B��2�� C��3�� D��4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com