
【题目】如图,∠AOB=∠COD=90°,OE平分∠AOC,∠AOD=120°.

(1)求∠BOC的度数;
(2)求∠BOE的度数.
【答案】(1)60°;(2)15°.
【解析】
试题分析:(1)根据周角等于360°列式进行计算即可得解;
(2)先求出∠AOC的度数,然后根据角平分线的定义求出∠COE的度数,再根据∠BOE=∠COE﹣∠BOC,代入数据进行计算即可得解.
解:(1)∵∠AOB=∠COD=90°,∠AOD=120°,
∴∠BOC=360°﹣∠AOB﹣∠COD﹣∠AOD,
=360°﹣90°﹣90°﹣120°,
=60°;
(2)∵∠AOB=90°,∠BOC=60°,
∴∠AOC=∠AOB+∠BOC=90°+60°=150°,
∵OE平分∠AOC,
∴∠COE=![]() AOC=
AOC=![]() ×150°=75°,
×150°=75°,
∴∠BOE=∠COE﹣∠BOC=75°﹣60°=15°.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:
【题目】已知三角形的两边长分别为4cm和9cm,则下列长度的四条线段中能作为第三边的是( )
A. 13cm B. 6cm C. 5cm D. 4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题背景】
在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,试探究图1中线段BE、EF、FD之间的数量关系.
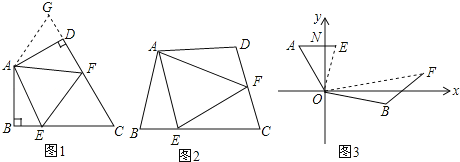
【初步探索】
小亮同学认为:延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,则可得到 BE、EF、FD之间的数量关系是 .
【探索延伸】
在四边形ABCD中如图2,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,∠EAF=![]() ∠BAD,上述结论是否任然成立?说明理由.
∠BAD,上述结论是否任然成立?说明理由.
【结论运用】
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角(∠EOF)为70°,试求此时两舰艇之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A在第二象限,以A为顶点的抛物线经过原点,与x轴负半轴交于点B,对称轴为直线x=﹣1,点C在抛物线上,且位于点A、B之间(C不与A、B重合).若△ABC的周长为m,四边形AOBC的周长为 (用含m的式子表示).
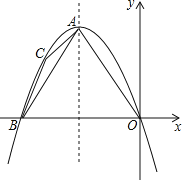
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校九年级(1)班所有学生参加2015年初中毕业生升学体育测试,根据测试评分标准,将他们的成绩进行统计后分为A、B、C、D四等,并绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:

(1)九年级(1)班参加体育测试的学生有 人;
(2)将条形统计图补充完整;
(3)在扇形统计图中,等级B部分所占的百分比是 ,等级C对应的圆心角的度数为 ;
(4)若该校九年级学生共有550人参加体育测试,估计达到A级和B级的学生共有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年某省遭遇历史罕见的夏秋东连旱,全省因灾造成直接经济损失68.77亿元,用科学计数法表示为( )
A、68.77×109 B、6.877×109 C、6.877×1010 D、6877×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.

(1)请画出平移后的△A′B′C′,并求△A′B′C′的面积;
(2)若连接AA′,CC′,则这两条线段之间的关系是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com