
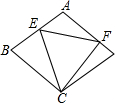
 如图,E,F是菱形ABCD边AB与AD上的动点,在点E,F移动的过程中,保持AE=FD,若∠B=60°,AB=4,则△CEF的面积是否存在最小值?如果存在,求出这个值;如果不存在,请说明理由.
如图,E,F是菱形ABCD边AB与AD上的动点,在点E,F移动的过程中,保持AE=FD,若∠B=60°,AB=4,则△CEF的面积是否存在最小值?如果存在,求出这个值;如果不存在,请说明理由. 分析 首先证明△AFC≌△BEC(SAS)推出CF=CE,△ECF是等边三角形,当CE⊥AB时,CE的长最小,最小值为$\frac{\sqrt{3}}{2}$×6=3$\sqrt{3}$,即可推出△ECF的面积的最小值是$\frac{\sqrt{3}}{4}$•(3$\sqrt{3}$)2;
解答 解:连接CA,如右图所示,
∵四边形ABCD是菱形,∠B=60°,AE=DF,
∴AB=BC=CD=DA,∠BAD=120°,
∴∠FAC=60°,BE=AF,AB=BC=AC,
在△AFC和△BEC中,
$\left\{\begin{array}{l}{AF=BE}\\{∠FAC=∠B}\\{AC=BC}\end{array}\right.$,
∴△AFC≌△BEC(SAS)
∴CF=CE,∠ACF=∠BCE,
又∵∠BCE+∠ECA=60°,
∴∠ECA+∠ACF=60°,
∴△ECF是等边三角形;
当CE⊥AB时,CE的长最小,最小值为$\frac{\sqrt{3}}{2}$×6=3$\sqrt{3}$,
∴△ECF的面积的最小值是$\frac{\sqrt{3}}{4}$•(3$\sqrt{3}$)2=$\frac{27\sqrt{3}}{4}$.
点评 本题考查菱形的性质、最短路线问题、等边三角形的判定和性质、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,学会利用垂线段最短解决最短问题,属于中考常考题型.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | -1 | D. | 1或-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,小林在一块长为6m,宽为4m,一边靠墙的矩形小花园ABCD周围栽种了一种花来装饰,这种花的边框宽为20cm,边框内外边缘所围成的两个矩形相似吗?
如图所示,小林在一块长为6m,宽为4m,一边靠墙的矩形小花园ABCD周围栽种了一种花来装饰,这种花的边框宽为20cm,边框内外边缘所围成的两个矩形相似吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知反比例函数y1=$\frac{k_1}{x}$与一次函数y2=k2x+b的图象交于点A(1,8),B(-4,m)两点.
如图,已知反比例函数y1=$\frac{k_1}{x}$与一次函数y2=k2x+b的图象交于点A(1,8),B(-4,m)两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com