
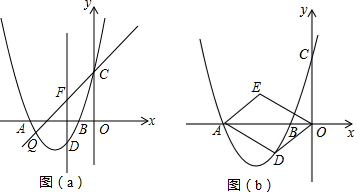
���� ��1����ϵ�A��B���������ô���ϵ����������������ߵĽ���ʽ��
��2���ټ�����ڣ������D�����꣮����һ�κ����������ߵĽ���ʽ�ɷ����飬�ⷽ���������Q��C�����꣬�ɵ㵽ֱ�ߵľ��빫ʽ�����D��ֱ��CQ�ľ���͵�C��ֱ��DF�ľ��룬���ݶ��ߵı�����ϵ�ó�����m�ĺ�����ֵ���ŵ�һԪ���η��̣��ⷽ�̵ó�m��ֵ���ɴ˼��ɵó���D�����ꣻ
�ڸ��������ߵĽ���ʽ�ҳ��䶥�����꣬��Ϻ���ͼ��Ѱ�ҳ�����D�����������ֵΪ$\frac{27}{16}$ʱ����������ĵ�D�����������÷ָ�ͼ�η����ƽ���ı��ε����S���ٽ�y=��$\frac{27}{16}$���������߽���ʽ�����D�����꼴�ɣ�
��� �⣺��1������A��-4��0����B��-1��0������������y=ax2+bx+3�У�
�ã�$\left\{\begin{array}{l}{0=16a-4b+3}\\{0=a-b+3}\end{array}\right.$����ã�$\left\{\begin{array}{l}{a=\frac{3}{4}}\\{b=\frac{15}{4}}\end{array}\right.$��
�������ߵĽ���ʽΪy=$\frac{3}{4}{x}^{2}$+$\frac{15}{4}$x+3��
��2���ټ�����ڣ����D������Ϊ��m��$\frac{3}{4}$m2+$\frac{15}{4}$m+3����m��0����
����$\left\{\begin{array}{l}{y=x+3}\\{y=\frac{3}{4}{x}^{2}+\frac{15}{4}x+3}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=0}\\{y=3}\end{array}\right.$��$\left\{\begin{array}{l}{x=-\frac{11}{3}}\\{y=-\frac{2}{3}}\end{array}\right.$��
���C��������0��3����
ֱ��CQ�Ľ���ʽΪy=x+3�ɱ���Ϊx-y+3=0��
ֱ��DF�Ľ���ʽΪx=m��
��D��ֱ��CQ�ľ���d1=$\frac{|m-��\frac{3}{4}{m}^{2}+\frac{15}{4}m+3��+3|}{\sqrt{{1}^{2}+��-1��^{2}}}$=$\frac{|\frac{3}{4}{m}^{2}+\frac{11}{4}m|}{\sqrt{2}}$��
��C��ֱ��DF�ľ���d2=|0-m|=-m��
��d1��d2=$\sqrt{2}$��1��
��$\frac{|\frac{3}{4}{m}^{2}+\frac{11}{4}m|}{\sqrt{2}}$=-$\sqrt{2}$m��
��ã�m1=-$\frac{19}{3}$��m2=0����ȥ����m3=-1��
����D��������-$\frac{19}{3}$��$\frac{28}{3}$����-1��0����
����������ĵ�D��ʹ��D��ֱ��CQ�ľ������C��ֱ��DF�ľ���֮��Ϊ$\sqrt{2}$��1����ʱ��D������Ϊ��-$\frac{19}{3}$��$\frac{28}{3}$����-1��0����
�ڡ������ߵĽ���ʽΪy=$\frac{3}{4}{x}^{2}$+$\frac{15}{4}$x+3=$\frac{3}{4}$$��x+\frac{5}{2}��^{2}$-$\frac{27}{16}$��
��������ߵĶ�������Ϊ��-$\frac{5}{2}$��-$\frac{27}{16}$����
���D��x��ľ���Ϊh��
�֡ߵ�C������Ϊ��0��3����$\frac{27}{16}$��3��
�൱0��h��$\frac{27}{16}$ʱ����������ĵ�D��4������h=$\frac{27}{16}$ʱ����������ĵ�D��3������$\frac{27}{16}$��h��3ʱ����������ĵ�D��2������h��3ʱ����������ĵ�D��1����
��h=$\frac{27}{16}$����ʱS=AO•h=4��$\frac{27}{16}$=$\frac{27}{4}$��
��i����y=-$\frac{27}{16}$����y=$\frac{3}{4}{x}^{2}$+$\frac{15}{4}$x+3�еã�$\frac{3}{4}{x}^{2}$+$\frac{15}{4}$x+3=-$\frac{27}{16}$��
��ã�x=-$\frac{5}{2}$��
��ʱ��D������Ϊ��-$\frac{5}{2}$��-$\frac{27}{16}$����
��ii����y=$\frac{27}{16}$����y=$\frac{3}{4}{x}^{2}$+$\frac{15}{4}$x+3�еã�$\frac{3}{4}{x}^{2}$+$\frac{15}{4}$x+3=$\frac{27}{16}$��
��ã�x1=-$\frac{5+3\sqrt{2}}{2}$��x2=-$\frac{5-3\sqrt{2}}{2}$��
��ʱ��D������Ϊ��-$\frac{5+3\sqrt{2}}{2}$��$\frac{27}{16}$����-$\frac{5-3\sqrt{2}}{2}$��$\frac{27}{16}$����
���Ͽ�֪����?ODAE�����SΪ$\frac{27}{4}$ʱ�����������ĵ�Dǡ����3������ʱ��D������Ϊ��-$\frac{5}{2}$��-$\frac{27}{16}$������-$\frac{5+3\sqrt{2}}{2}$��$\frac{27}{16}$���ͣ�-$\frac{5-3\sqrt{2}}{2}$��$\frac{27}{16}$����
���� ���⿼���˴���ϵ������������ʽ���㵽ֱ�ߵľ��롢���Ԫ���η����顢��һԪ���η����Լ������ε������ʽ������Ĺؼ��ǣ���1�����ô���ϵ������������ʽ����2���ٸ��ݱ�����ϵ�ҳ�����m�ĺ�����ֵ���ŵ�һԪ���η��̣���ȷ����D��x��ľ��루��D��������ľ���ֵ�������������е��⣬��1��û�Ѷȣ���2�����ѶȲ���������������˵㵽ֱ�ߵľ��룬����Ϊ������ã����ѶȲ������Է������������ʱ����Ϻ���ͼ���������ν�ϣ�ȷ����D��x��ľ����ǹؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ���䣨�꣩ | 12 | 13 | 14 | 15 |
| ���������� | 2 | 4 | 6 | 8 |
| A�� | 13 | B�� | 14 | C�� | 13.5 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����������ȵ�ʵ���� | B�� | ��������ȵ�ʵ���� | ||
| C�� | ��һ��ʵ���� | D�� | û��ʵ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
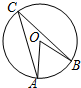 ��ͼ����֪A��B��C�ڡ�O�ϣ���ACB=30�㣬���AOB���ڣ�������
��ͼ����֪A��B��C�ڡ�O�ϣ���ACB=30�㣬���AOB���ڣ�������| A�� | 60�� | B�� | 50�� | C�� | 45�� | D�� | 30�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
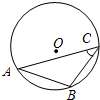 ��ͼ����C�ǡ�O�ϵĶ��㣬��AB=4����C=45�㣬��S��ABC�����ֵ�ǣ�������
��ͼ����C�ǡ�O�ϵĶ��㣬��AB=4����C=45�㣬��S��ABC�����ֵ�ǣ�������| A�� | $2\sqrt{2}$+4 | B�� | 8 | C�� | $2\sqrt{3}$+4 | D�� | 4$\sqrt{2}$+4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ֱ��y1=$\frac{1}{2}$x+2��˫����y2=$\frac{6}{x}$����A��2��m����B��-6��n�����㣮��y1��y2ʱ��x��ȡֵ��Χ�ǣ�������
��ͼ��ֱ��y1=$\frac{1}{2}$x+2��˫����y2=$\frac{6}{x}$����A��2��m����B��-6��n�����㣮��y1��y2ʱ��x��ȡֵ��Χ�ǣ�������| A�� | x��-6��0��x��2 | B�� | -6��x��0��x��2 | C�� | x��-6��0��x��2 | D�� | -6��x��2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com