Question

【题目】如图，在ABCD中，点E是DC的中点，连接AE，并延长交BC的延长线于点F．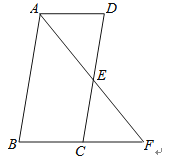

（1）求证：△ADE和△CEF的面积相等
（2）若AB=2AD，试说明AF恰好是∠BAD的平分线

Answer 1

【答案】
（1）

证明：∵四边形ABCD是平行四边形，

∴AD∥BC，

∴∠DAE=∠F，

∵点E是DC的中点，

∴CE=DE，

在△AED和△FEC

，

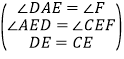∴△AED≌△FEC（AAS），

∴△ADE和△CEF的面积相等

（2）

证明∵四边形ABCD是平行四边形，

∴AD=BC，

∵△AED≌△FEC，

∴AD=CF，

∴AD=BC=CF，

∵AB=2AD，

∴AB=2BC=BF，

∴∠BAF=∠F，

又∵∠DAE=∠F，

∴∠BAF=∠DAE，

即AF是∠BAD的平分线．

【解析】（1）首先根据平行四边形的性质可得AD∥BC，根据平行线的性质可得∠DAE=∠F，然后再证明△AED≌△FEC可得结论；
（2）首先根据平行四边形的性质可得AD=BC，根据全等三角形的性质可得AD=CF，然后再证明AB=BF，进而可得∠BAF=∠F，再由∠DAE=∠F，可得∠BAF=∠DAE，进而可得AF恰好是∠BAD的平分线．