

���� ��1���������ε����ʣ��ó����ۣ�ֱ���жϳ���BCE�ա�CDF�������û���ó���CPE=90�㼴�ɣ�
��2���������жϳ���P���˶��켣��Ȼ���û�����ʽ���㼴�ɣ�
��3���������ж�����P���˶��켣���Ե�OΪԲ�ģ�OAΪ�뾶������֮һԲ�����㼴�ɣ�
��� �⣺��1����BE=CF��BE��CF��
���ɣ�
���ı���ABCD�������Σ�
��BC=CD����BCE=��CDF��
�ڡ�BCE�͡�CDF�У�
$\left\{\begin{array}{l}{BC=CD}\\{��BCE=��CDF}\\{CF=DF}\end{array}\right.$��
���BCE�ա�CDF��
��BE=CF����CBE=��DCF��
�ߡ�CBE+��BEC=90�㣬
���DCF+��BEC=90�㣬
���CPE=90�㣬
��BE��CF��
����BE=CF����BE��CF��
����ͼ1��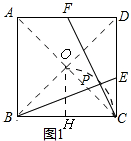
�ɢ�֪��BE��CF��
���ڵ�E�ӵ�C����D�Ĺ����У�ʼ���С�BPC=90�㣬
��BC=4��
���P�˶���·������BCΪֱ����$\frac{1}{4}$Բ���ϣ�
���P���˶�·����Ϊ$\frac{1}{4}$��2�С�2=�У�
��3����ͼ2��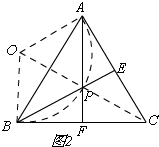
��P����OΪԲ�ģ�OAΪ�뾶��$\frac{1}{3}$Բ���ϣ�
����E�˶���AC�е�ʱ����FҲ�˶���BC���е㣬��ʱ��P����$\widehat{AB}$���е㣬
��ʱ��ABPΪ���������Σ���ABP=��BAP=30�㣬
���AOB=120�㣬
��AB=6��
��OA=2$\sqrt{3}$��
���P��·��Ϊ$\frac{120�С�2\sqrt{3}}{180}$=$\frac{4\sqrt{3}}{3}$�У�
���� �������ı����ۺ��⣬��Ҫ�����������ε����ʣ�ȫ�������ε��ж������ʣ��������⣬�Ȿ��Ĺؼ���ȷ������P���˶��켣��Ҳ�DZ�����ѵ㣮


 ͬ������ϵ�д�
ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
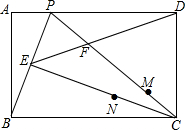 ��ͼ���ھ���ABCD�У�PΪAD��һ�㣬����BP��CP����C��CE��BP�ڵ�E������ED��PC�ڵ�F��
��ͼ���ھ���ABCD�У�PΪAD��һ�㣬����BP��CP����C��CE��BP�ڵ�E������ED��PC�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
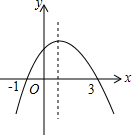 ��ͼ��ʾ�Ƕ��κ���y=ax2+bx+c��a��0����ͼ����������˵����
��ͼ��ʾ�Ƕ��κ���y=ax2+bx+c��a��0����ͼ����������˵����| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
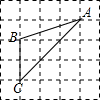 ��ͼ����֪��ABC������������ڸ���ϣ���cosA��ֵΪ$\frac{2\sqrt{5}}{5}$��
��ͼ����֪��ABC������������ڸ���ϣ���cosA��ֵΪ$\frac{2\sqrt{5}}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4a+5b=9ab | B�� | ��a3��5=a15 | C�� | a4•a2=a8 | D�� | a6��a3=a2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ڵ����ϵĵ�A���������B������Ϊ���ȣ�AC=7�ף�������BCΪ��������
��ͼ���ڵ����ϵĵ�A���������B������Ϊ���ȣ�AC=7�ף�������BCΪ��������| A�� | 7sin���� | B�� | 7cos���� | C�� | 7tan���� | D�� | ��7+������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x-$\frac{1}{4}$��2=$\frac{9}{16}$ | B�� | ��x+$\frac{1}{4}$��2=$\frac{9}{16}$ | C�� | ��x-$\frac{1}{2}$��2=$\frac{5}{4}$ | D�� | ��x+$\frac{1}{2}$��2=$\frac{5}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ָ������ | 21=2 | 22=4 | 23=8 | �� | 31=3 | 32=9 | 33=27 | �� |
| ������ | log22=1 | log24=2 | log28=3 | �� | log33=1 | log39=2 | log327=3 | �� |
| A�� | �٢� | B�� | �٢� | C�� | �ڢ� | D�� | �٢ڢ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com