
| A. | |-2| | B. | 20 | C. | 2-1 | D. | $\sqrt{2}$ |
分析 正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小,首先求出|-2|,20,2-1的值是多少,然后根据实数比较大小的方法判断即可.
解答 解:|-2|=2,20=1,2-1=0.5,
∵$0.5<1<\sqrt{2}<2$,
∴${2}^{-1}{<2}^{0}<\sqrt{2}<|-2|$,
∴在|-2|,20,2-1,$\sqrt{2}$这四个数中,最大的数是|-2|.
故选:A.
点评 (1)此题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是要明确:正实数>0>负实数,两个负实数绝对值大的反而小.
(2)此题还考查了负整数指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a-p=$\frac{1}{{a}^{p}}$(a≠0,p为正整数);②计算负整数指数幂时,一定要根据负整数指数幂的意义计算;③当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.
(3)此题还考查了零指数幂的运算,要熟练掌握,解答此题的关键是要明确:①a0=1(a≠0);②00≠1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
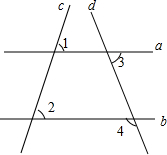 直线a、b、c、d的位置如图所示,如果∠1=58°,∠2=58°,∠3=70°,那么∠4等于( )
直线a、b、c、d的位置如图所示,如果∠1=58°,∠2=58°,∠3=70°,那么∠4等于( )| A. | 58° | B. | 70° | C. | 110° | D. | 116° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 5 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com