
【题目】甲、乙两辆汽车同时分别从A、B两城沿同一条高速公路匀速驶向C城.已知A、C两城的距离为360km,B、C两城的距离为320km,甲车比乙车的速度快10km/h,结果两辆车同时到达C城.设乙车的速度为xkm/h.
(1)根据题意填写下表:
行驶的路程(km) | 速度(km/h) | 所需时间(h) | |
甲车 | 360 |
|
|
乙车 | 320 | x |
|
(2)求甲、乙两车的速度.
【答案】(1)
行驶的路程(km) | 速度(km/h) | 所需时间(h) | |
甲车 | 360 | x+10 |
|
乙车 | 320 | x |
|
(2)甲的速度是90千米/时,乙的速度是80千米/时.
【解析】
试题分析:(1)设乙的速度是x千米/时,那么甲的速度是(x+10)千米/时,根据时间=![]() 可求甲、乙两辆汽车所需时间;
可求甲、乙两辆汽车所需时间;
(2)路程知道,且同时到达,可以时间做为等量关系列方程求解.
解:(1)甲的速度是(x+10)千米/时,
甲车所需时间是![]() ,乙车所需时间是
,乙车所需时间是![]() ;
;
行驶的路程(km) | 速度(km/h) | 所需时间(h) | |
甲车 | 360 | x+10 |
|
乙车 | 320 | x |
|
(2)乙的速度是x千米/时,甲的速度是(x+10)千米/时,依题意得:
![]() =
=![]() ,
,
解得x=80,
经检验:x=80是原方程的解,
x+10=90,
答:甲的速度是90千米/时,乙的速度是80千米/时.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
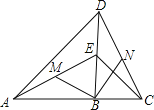
【题目】如图,已知点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M,N分别是AE,CD的中点,现有如下结论:①∠ABD=∠BDN;②MB=NB;③MB⊥NB;④S△ABM=S△BCN,其中正确的结论是 (只填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是直线AB上一点,OC为任意一条射线,OD平分∠BOC,OE平分∠AOC.

(1)指出图中∠AOD与∠BOE的补角;
(2)试判断∠COD与∠COE具有怎样的数量关系.并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1) ![]() (2) 12+(-8)+11+(-2)+(-12)
(2) 12+(-8)+11+(-2)+(-12)
![]() +
+![]() (4) (-24)÷2×(-3)÷(-6)
(4) (-24)÷2×(-3)÷(-6)
(5)![]() (6)(-4)×(-2
(6)(-4)×(-2![]() )+(-8)×(-2
)+(-8)×(-2![]() )+12×(-2
)+12×(-2![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是假命题的是( )
A.若|a|=|b|,则a=b
B.两直线平行,同位角相等
C.对顶角相等
D.若b2﹣4ac>0,则方程ax2+bx+c=0(a≠0)有两个不等的实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
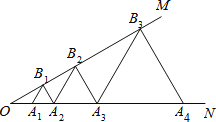
【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA2=4,则△AnBnAn+1的边长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[背景知识]数轴是初中数学的一个重要工具,利用数轴可以将数与形完美的结合.研究数轴我们发现了许多重要的规律:数轴上A点、B点表示的数为a、b,则A,B两点之间的距离AB=|a﹣b|,若a>b,则可简化为AB=a﹣b;线段AB的中点M表示的数为![]() .
.
[问题情境]
已知数轴上有A、B两点,分别表示的数为﹣10,8,点A以每秒3个单位的速度沿数轴向右匀速运动,点B以每秒2个单位向左匀速运动.设运动时间为t秒(t>0).
![]()
[综合运用]
(1)运动开始前,A、B两点的距离为 ;线段AB的中点M所表示的数 .
(2)点A运动t秒后所在位置的点表示的数为 ;点B运动t秒后所在位置的点表示的数为 ;(用含t的代数式表示)
(3)它们按上述方式运动,A、B两点经过多少秒会相遇,相遇点所表示的数是什么?
(4)若A,B按上述方式继续运动下去,线段AB的中点M能否与原点重合?若能,求出运动时间,并直接写出中点M的运动方向和运动速度;若不能,请说明理由.(当A,B两点重合,则中点M也与A,B两点重合)
查看答案和解析>>
科目:初中数学 来源: 题型:
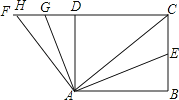
【题目】如图,在矩形ABCD中,AC是对角线,点E是BC的中点,连接AE,AB=4,BC=3,将∠BAE绕点A逆时针旋转,使∠BAE的两边分别与线段CD的延长线相交于点G,H.当AH=AC时,CG= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com