
【题目】如图1,E为矩形ABCD边AD上一点,点P从点B沿折线BE﹣ED﹣DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.若点P、Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm)2.已知y与t的函数关系图象如图2,则下列结论错误的是( )
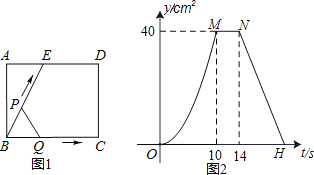
A.AE=6cm
B.sin∠EBC=0.8
C.当 0<t≤10 时,y=0.4t2
D.当 t=12s 时,△PBQ 是等腰三角形
【答案】D
【解析】
根据函数图象可知在点(10,40)至点(14,40)区间,△BPQ的面积不变,因此可推论BC=BE,由此分析动点P的运动过程如下:在BE段,BP=BQ;持续时间10s,则BE=BC=10;y是t的二次函数;在ED段,y=40是定值,持续时间4s,则ED=4;在DC段,y持续减小直至为0,y是t的一次函数.
解: A正确.理由如下:
分析函数图象可知,BC=10cm,ED=4cm,故AE=AD-ED=BC-ED=10-4=6cm;
B正确.理由如下:
如图所示,连接EC,过点E作EF⊥BC于点F,
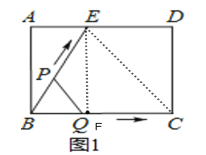
由函数图象可知,![]() ,
,
∴EF=8,
∴![]() ;
;
C正确.理由如下:
如图所示,过点P作PG⊥BQ于点G,
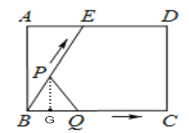
∵BQ=BP=t,
∴![]() .
.
D错误.理由如下:
当t=12s时,点Q与点C重合,点P运动到ED的中点,设为N,如图所示,连接NB,NC.
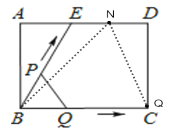
此时AN=8,ND=2,由勾股定理求得:![]() ,
,
∵BC=10,
∴△BCN不是等腰三角形,即此时△PBQ不是等腰三角形.
故选:D.


科目:初中数学 来源: 题型:
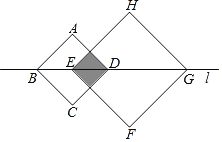
【题目】如图,正方形ABCD和正方形EFGH的对角线BD,EG都在直线l上,将正方形ABCD沿着直线l从点D与点E重合开始向右平移,直到点B与点G重合为止,设点D平移的距离为x,![]() ,
,![]() ,两个正方形重合部分的面积为S,则S关于x的函数图象大致为( )
,两个正方形重合部分的面积为S,则S关于x的函数图象大致为( )
A.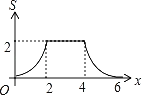 B.
B.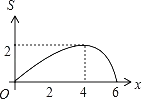
C.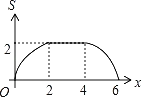 D.
D.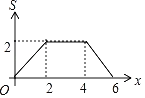
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校随机抽查了部分九年级女生进行1分钟仰卧起坐测试,并将测试的结果绘制成了如图的不完整的统计表和频数分布直方图(注:在频数分布直方图中,每组含左端点,但不含右端点):
仰卧起坐次数的范围(次) | 15~20 | 20~25 | 25~30 | 30~35 |
频数 | 3 | 10 | 12 |
|
频率 |
|
|
|
|

(1)30~35的频数是 、25~30的频率是 .并把统计图补充完整;
(2)被抽查的所有女同学仰卧起坐次数的中位数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() .
.
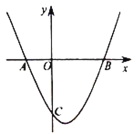
(1)求![]() 点坐标;
点坐标;
(2)若对于每一个给定的![]() 的值,它所对应的函数值都不小于
的值,它所对应的函数值都不小于![]() ,求
,求![]() 的取值范围.
的取值范围.
(3)直线![]() 经过点
经过点![]() .
.
①求直线和抛物线的解析式;
②设抛物线与![]() 轴的交点为
轴的交点为![]() ,过点
,过点![]() 作直线
作直线![]() 轴,将抛物线在
轴,将抛物线在![]() 轴左侧的部分沿直线
轴左侧的部分沿直线![]() 翻折,抛物线的其余部分保持不变,得到一个新图像,请你结合新图像回答:
翻折,抛物线的其余部分保持不变,得到一个新图像,请你结合新图像回答:
当直线![]() 与新图像只有一个公共点
与新图像只有一个公共点![]() 且
且![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() 的图象经过点(
的图象经过点(![]() ,
,![]() )和(
)和(![]() ,
,![]() ),完成下面问题:
),完成下面问题:
(1)求函数![]() 的表达式;
的表达式;
(2)在给出的平面直角坐标系中,请用适当的方法画出这个函数的图象,并写出这个函数的一条性质;
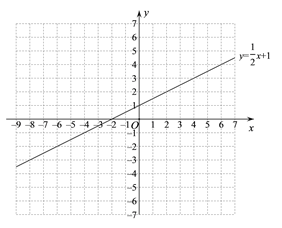
(3)已知函数![]() 的图象如图所示,结合你所画出
的图象如图所示,结合你所画出![]() 的图象,直接写出
的图象,直接写出![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=![]() (m为常数,且n≠0)的图象交于点A(﹣3,1)、B(1,n).
(m为常数,且n≠0)的图象交于点A(﹣3,1)、B(1,n).
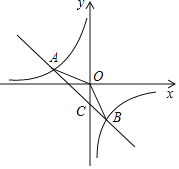
(1)求反比例函数和一次函数的解析式;
(2)连结0A、OB,求△AOB的面积;
(3)直接写出当y1<y2<0时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程.
已知:直线l及直线l外一点P.
求作:直线![]() ,使得
,使得![]() .
.
作法:如图,
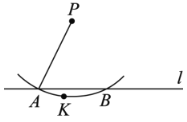
①任意取一点K,使点K和点P在直线l的两旁;
②以P为圆心,![]() 长为半径画弧,交l于点
长为半径画弧,交l于点![]() ,连接
,连接![]() ;
;
③分别以点![]() 为圆心,以
为圆心,以![]() 长为半径画弧,两弧相交于点Q(点Q和点A在直线
长为半径画弧,两弧相交于点Q(点Q和点A在直线![]() 的两旁);
的两旁);
④作直线![]() .
.
所以直线![]() 就是所求作的直线.
就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接![]() ,
,
![]() ______,
______,![]() ______,
______,
![]() 四边形
四边形![]() 是平行四边形(__________)(填推理依据).
是平行四边形(__________)(填推理依据).
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
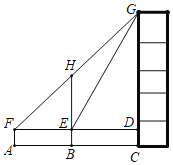
【题目】如图,某数学兴趣小组为测量一颗古树![]() 和教学楼
和教学楼![]() 的高,先在处用高15米的测角仪
的高,先在处用高15米的测角仪![]() 测得古树顶端
测得古树顶端![]() 的仰角
的仰角![]() 为45°,此时教学楼顶端
为45°,此时教学楼顶端![]() 恰好在视线
恰好在视线![]() 上,再向前走10米到达
上,再向前走10米到达![]() 处,又测得教学楼顶端
处,又测得教学楼顶端![]() 的仰角
的仰角![]() 为60°,点
为60°,点![]() 、
、![]() 、
、![]() 三点在同一水平线上.
三点在同一水平线上.
(1)求古树![]() 的高;
的高;
(2)求教学楼![]() 的高.(参考数据:
的高.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组要测量一栋五层居民楼CD的高度,该楼底层为车库,高2.5米;上面五层居住,每层高度相等,测角仪支架离地1.5米,在A处测得五楼顶部点D的仰角为60°,在B处测得四楼顶部点E的仰角为30°,AB=14米,求居民楼的高度.(精确到0.1米,参考数据:![]() ≈1.73)
≈1.73)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com