
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() .
.
(1)求![]() 点坐标;
点坐标;
(2)若对于每一个给定的![]() 的值,它所对应的函数值都不小于
的值,它所对应的函数值都不小于![]() ,求
,求![]() 的取值范围.
的取值范围.
(3)直线![]() 经过点
经过点![]() .
.
①求直线和抛物线的解析式;
②设抛物线与![]() 轴的交点为
轴的交点为![]() ,过点
,过点![]() 作直线
作直线![]() 轴,将抛物线在
轴,将抛物线在![]() 轴左侧的部分沿直线
轴左侧的部分沿直线![]() 翻折,抛物线的其余部分保持不变,得到一个新图像,请你结合新图像回答:
翻折,抛物线的其余部分保持不变,得到一个新图像,请你结合新图像回答:
当直线![]() 与新图像只有一个公共点
与新图像只有一个公共点![]() 且
且![]() 时,求
时,求![]() 的取值范围.
的取值范围.
【答案】(1)点B的坐标为(4,0);(2)0<m≤![]() ;(3)①直线的解析式为y=
;(3)①直线的解析式为y=![]() x-2;②b的取值范围为-4<b≤5或b<-
x-2;②b的取值范围为-4<b≤5或b<-![]() .
.
【解析】
(1)由抛物线的解析式可知它的对称轴是x=1,从而可得答案;
(2)由题意得到抛物线的开口方向,结合抛物线的顶点坐标可得答案;
(3)①利用已知条件建立关于![]() 的方程组,从而可得答案;
的方程组,从而可得答案;
②求解![]() 过抛物线上纵坐标为
过抛物线上纵坐标为![]() 的点时,
的点时,![]() 的值,再判断
的值,再判断![]() (b<-4)与函数 y=
(b<-4)与函数 y=![]() x2-x-4(x>0)的图像仅有一个公共点P时,
x2-x-4(x>0)的图像仅有一个公共点P时,![]() 的值,结合图像可得答案.
的值,结合图像可得答案.
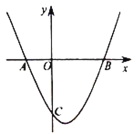
解:(1)依题意,可得抛物线的对称轴为:x=1.
∵抛物线与x轴交于A、B两点,点A的坐标为(-2,0),
∴点B的坐标为(4,0).
(2)∵点A在二次函数y=mx2-2mx+n的图像上,
∴0=4m+4m+n.即n=-8m.
∴y=mx2-2mx-8m=![]() ,顶点坐标是(1,-9m)
,顶点坐标是(1,-9m)
∵若对于每一个给定的x的值,它所对应的函数值都不小于-5,
∴![]()
即0<m≤![]() .
.
(3)①∵点B在直线y=![]() x+4m+n上,∴0=2+4m+n.
x+4m+n上,∴0=2+4m+n.
又 n=-8m,
∴m=![]() ,n=-4.
,n=-4.
抛物线的解析式为y=![]() x2-x-4,
x2-x-4,
直线的解析式为y=![]() x-2.
x-2.
②由y=![]() x2-x-4得:抛物线与y轴的交点为C(0,-4).
x2-x-4得:抛物线与y轴的交点为C(0,-4).
直线l:y=-4,依题意翻折后的图像如图所示.
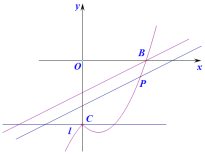
令y=8,则 ![]() x2-x-4=8.解得x1=-4,x2=6.
x2-x-4=8.解得x1=-4,x2=6.
∴新图像经过点(6,8).
当直线y=![]() x+b经过(6,8)点时,可得b=5.
x+b经过(6,8)点时,可得b=5.
当直线y=![]() x+b经过C点时,可得b=-4.
x+b经过C点时,可得b=-4.
当直线y=![]() x+b(b<-4)与函数 y=
x+b(b<-4)与函数 y=![]() x2-x-4(x>0)的图像仅有一个公共点P时,
x2-x-4(x>0)的图像仅有一个公共点P时,
也就是方程![]() x2-x-4=
x2-x-4=![]() x+b有相等的实数根.
x+b有相等的实数根.
整理方程,得 x2-3x-(8+2b)=0.
由根的判别式=(-3)2+4(8+2b)=8b+41=0,得b=-![]() .
.
结合图像可知,b的取值范围为-4<b≤5或b<-![]() .
.
【点晴】
本题考查的二次函数的基本性质,以及用待定系数法求函数的解析式,同时考查了函数只有一个交点时,字母的取值范围,从图像中获取信息就是解题的关键.


科目:初中数学 来源: 题型:
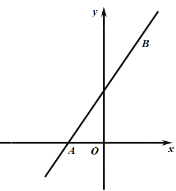
【题目】如图,在平面直角坐标系中,点![]() 为原点,直线
为原点,直线![]() (
(![]() 为常数,且
为常数,且![]() )经过点
)经过点![]() ,交
,交![]() 轴于点
轴于点![]() ,已知点
,已知点![]() 的坐标为
的坐标为![]()
![]() 求
求![]() 的值;
的值;
![]() 过点
过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,点
,点![]() 在
在![]() 的延长线上,连接
的延长线上,连接![]() ,且
,且![]() 在线段
在线段![]() 上分别取点
上分别取点![]() 使得
使得![]() ,连接
,连接![]() ,设点
,设点![]() 的纵坐标为
的纵坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式(不要求写出自变量
之间的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
![]() 在(2)的条件下,连接
在(2)的条件下,连接![]() ,当
,当![]() 时,点
时,点![]() 在线段
在线段![]() 上,连接
上,连接![]() 且
且![]() .求
.求![]() 的值.
的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】济南某中学在参加“创文明城,点赞泉城”书画比赛中,杨老师从全校30个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作鼎的数量进行了分析统计,制作了两幅不完整的统计图.

请根据以上信息,回答下列问题:
(l)杨老师采用的调查方式是 (填“普查”或“抽样调查”);
(2)请补充完整条形统计图,并计算扇形统计图中C班作品数量所对应的圆心角度数 .
(3)请估计全校共征集作品的什数.
(4)如果全枝征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一样等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
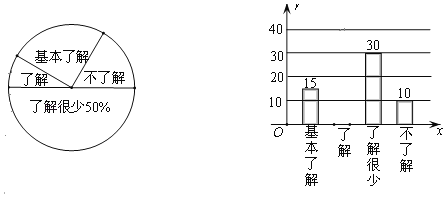
【题目】“食品安全”受到全社会的广泛关注,武汉市某中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 人,扇形统计图中“了解”部分所对应扇形的圆心角为 ;
(2)若从对食品安全知识达到“了解”程度的2个女生和2个男生中随机抽取2人参加食品安全知识竞赛,恰好抽到1个男生和1个女生的概率为 ;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有四位“抗疫”英雄(依次标记为![]() 、
、![]() 、
、![]() 、
、![]() ).为了让同学们了解他们的英雄事迹,张老师设计了如下活动:取四张完全相同的卡片,分别在正面写上
).为了让同学们了解他们的英雄事迹,张老师设计了如下活动:取四张完全相同的卡片,分别在正面写上![]() 、
、![]() 、
、![]() 、
、![]() 四个标号,然后背面朝上放置,搅匀后请一位同学从中随机抽取一张,记下标号后放回,要求大家依据抽到标号所对应的人物查找相应“抗疫”英雄资料.
四个标号,然后背面朝上放置,搅匀后请一位同学从中随机抽取一张,记下标号后放回,要求大家依据抽到标号所对应的人物查找相应“抗疫”英雄资料.
(1)班长在这四种卡片中随机抽到标号为![]() 的概率为___________;
的概率为___________;
(2)用树状图或列表法求小明和小亮两位同学抽到的卡片是不同“抗疫”英雄标号的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,AD与BC相交于点E,AF平分∠BAD,交BC于点F,交CD的延长线于点G.

(1)若∠G=29°,求∠ADC的度数;
(2)若点F是BC的中点,求证:AB=AD+CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,E为矩形ABCD边AD上一点,点P从点B沿折线BE﹣ED﹣DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.若点P、Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm)2.已知y与t的函数关系图象如图2,则下列结论错误的是( )
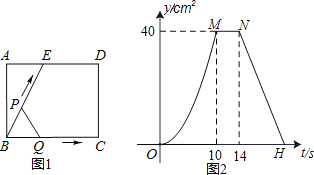
A.AE=6cm
B.sin∠EBC=0.8
C.当 0<t≤10 时,y=0.4t2
D.当 t=12s 时,△PBQ 是等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的点P和图形M,给出如下定义:Q为图形M上任意一点,如果
中的点P和图形M,给出如下定义:Q为图形M上任意一点,如果![]() 两点间的距离有最大值,那么称这个最大值为点P与图形M间的开距离,记作
两点间的距离有最大值,那么称这个最大值为点P与图形M间的开距离,记作![]() .已知直线
.已知直线![]() 与x轴交于点A,与y轴交于点B,
与x轴交于点A,与y轴交于点B,![]() 的半径为1.
的半径为1.
(1)若![]() ,
,
①求![]() 的值;
的值;
②若点C在直线![]() 上,求
上,求![]() 的最小值;
的最小值;
(2)以点A为中心,将线段![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,点E在线段
,点E在线段![]() 组成的图形上,若对于任意点E,总有
组成的图形上,若对于任意点E,总有![]() ,直接写出b的取值范围.
,直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴的一个交点
轴的一个交点![]() 在点
在点![]() 和
和![]() 之间,其部分图象如图所示,则以下结论:①
之间,其部分图象如图所示,则以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④方程以
;④方程以![]() 有两个的实根,其中正确的个数为( )
有两个的实根,其中正确的个数为( )
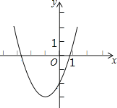
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com