
【题目】如图,AB∥CD,AD与BC相交于点E,AF平分∠BAD,交BC于点F,交CD的延长线于点G.

(1)若∠G=29°,求∠ADC的度数;
(2)若点F是BC的中点,求证:AB=AD+CD.
【答案】(1)58°;(2)详见解析
【解析】
(1)根据平行和角平分线,可推导出∠ADC=2∠G,从而得出∠ADC的大小;
(2)证△ABF≌△GCF,从而得出AB=GC,从而证AB=AD+CD.
证明:(1)∵AB∥CD,∴ ∠BAG=∠G, ∠BAD=∠ADC.
∵AF平分∠BAD,∴∠BAD=2∠BAG=2∠G.
∴∠ADC=∠BAD=2∠G .
∵∠G=29°,∴∠ADC=58°.
(2)∵AF平分∠BAD,∴∠BAG=∠DAG.
∵∠BAG=∠G, ∴∠DAG=∠G.
∴AD=GD.
∵点F是BC的中点,∴BF=CF.
在△ABF和△GCF中,
∵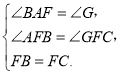
∴△ABF≌△GCF.
∴AB=GC.
∴AB=GD+CD=AD+CD.


科目:初中数学 来源: 题型:
【题目】新型冠状病毒肺炎疫情发生后,全社会的积极参与疫情防控工作下,才有了我们的平安复学.为了能在复学前将一批防疫物资送达校园,某运输公司组织了甲、乙两种货车,已知甲种货车比乙种货车每辆车多装20箱防疫物资,且甲种货车装运900箱防疫物资所用车辆与乙种货车装运600箱防疫物资所用的车辆相等,求甲、乙两种货车每辆车可装多少箱防疫物资?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() .直线
.直线![]() 经过点
经过点![]() ,
,![]() .
.
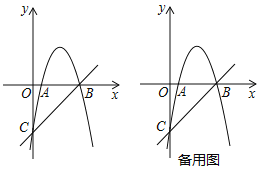
(1)求抛物线的解析式;
(2)过点![]() 的直线交直线
的直线交直线![]() 于点
于点![]() .
.
①当![]() 时,过抛物线上一动点
时,过抛物线上一动点![]() (不与点
(不与点![]() ,
,![]() 重合),作直线
重合),作直线![]() 的平行线交直线
的平行线交直线![]() 于点
于点![]() ,若以点
,若以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形,求点
为顶点的四边形是平行四边形,求点![]() 的横坐标;
的横坐标;
②连接![]() ,当直线
,当直线![]() 与直线
与直线![]() 的夹角等于
的夹角等于![]() 的
的![]() 倍时,请直接写出点
倍时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() .
.
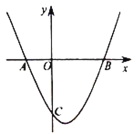
(1)求![]() 点坐标;
点坐标;
(2)若对于每一个给定的![]() 的值,它所对应的函数值都不小于
的值,它所对应的函数值都不小于![]() ,求
,求![]() 的取值范围.
的取值范围.
(3)直线![]() 经过点
经过点![]() .
.
①求直线和抛物线的解析式;
②设抛物线与![]() 轴的交点为
轴的交点为![]() ,过点
,过点![]() 作直线
作直线![]() 轴,将抛物线在
轴,将抛物线在![]() 轴左侧的部分沿直线
轴左侧的部分沿直线![]() 翻折,抛物线的其余部分保持不变,得到一个新图像,请你结合新图像回答:
翻折,抛物线的其余部分保持不变,得到一个新图像,请你结合新图像回答:
当直线![]() 与新图像只有一个公共点
与新图像只有一个公共点![]() 且
且![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E是边BC上一点,连接AE,过点E作EM⊥AE,交对角线AC于点M,过点M作MN⊥AB,垂足为N,连接NE.
(1)求证:AE=![]() NE+ME;
NE+ME;
(2)如图2,延长EM至点F,使EF=EA,连接AF,过点F作FH⊥DC,垂足为H.
猜想CH与FH存在的数量关系,并证明你的结论;
(3)在(2)的条件下,若点G是AF的中点,连接GH.当GH=CH时,直接写出GH与AC之间存在的数量关系.
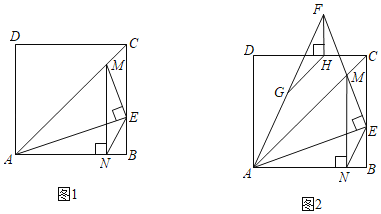
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=![]() (m为常数,且n≠0)的图象交于点A(﹣3,1)、B(1,n).
(m为常数,且n≠0)的图象交于点A(﹣3,1)、B(1,n).
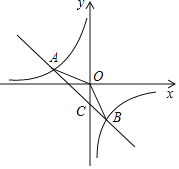
(1)求反比例函数和一次函数的解析式;
(2)连结0A、OB,求△AOB的面积;
(3)直接写出当y1<y2<0时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生开展义务植树活动,在活动结束后随机调查了40名学生每人植树的棵数,根据调查获取的样本数据,制作了条形统计图和扇形统计图.请根据相关信息,解答下列问题:
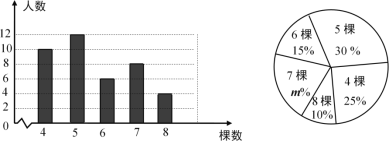
(1)扇形图中![]() 的值是_________;
的值是_________;
(2)求随机调查的40名学生每人植树棵数这组数据的平均数、众数和中位数;
(3)若本次活动九年级共有300名学生参加,估计植树超过6棵(不含6棵)的学生约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某开发商原计划对楼盘新房以每平方米4000元的销售价对外销售.现为了加快资金周转,对销售价经过两次下调后,决定在开盘之日以每平方米3240元的销售价进行促销.
(1)求销售价平均每次下调的百分率;
(2)开盘之日,开发商又给予以下两种优惠方案以供选择:方案①一次性送装修费每平方米50元;方案②打9.8折销售.张先生要购买一套100平方米的住房,试问哪种方案更优惠?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com