
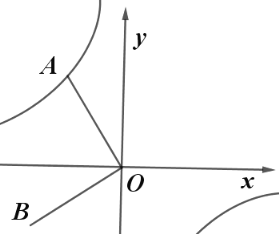
【题目】如图,已知点![]() 是反比例函数
是反比例函数![]() 图像上的一个动点,连接
图像上的一个动点,连接![]() ,若将线段
,若将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,则过点
,则过点![]() 的反比例函数解析式为__________.
的反比例函数解析式为__________.
【答案】![]()
【解析】
设A(m,n),过A作AC⊥x轴于C,过B作BD⊥x轴于D,得到AC=n,OC=-m,根据全等三角形的性质得到AC=OD=n,CO=BD=-m,于是得到结论.
∵点A是反比例函数![]() 的图象上的一个动点,设A(m,n),过A作AC⊥x轴于C,过B作BD⊥x轴于D,
的图象上的一个动点,设A(m,n),过A作AC⊥x轴于C,过B作BD⊥x轴于D,
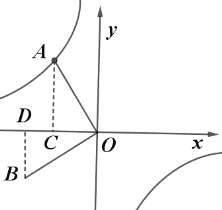
∴AC=n,OC=-m,
∴∠ACO=∠BDO=90°,
∵∠AOB=90°,
∴∠CAO+∠AOC=∠AOC+∠BOD=90°,
∴∠CAO=∠BOD,
在△ACO与△ODB中
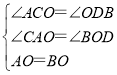 ,
,
∴△ACO≌△ODB,
∴AC=OD=n,CO=BD=-m,
∴B(-n,m),
∵mn=-4,
∴m(-n)=4,、
∴点B所在图象的函数表达式为![]() ,
,
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,二次函数y=﹣![]() x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
(1)填空:b= ,c= ;
(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;
(3)在x轴下方,该二次函数的图象上是否存在点M,使△PQM是以点P为直角顶点的等腰直角三角形?若存在,请求出运动时间t;若不存在,请说明理由;
(4)如图②,点N的坐标为(﹣![]() ,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标.
,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 是
是![]() 的内部一点,连接
的内部一点,连接![]() 、
、![]() 和
和![]() ,如果
,如果![]() 、
、![]() 和
和![]() 中有两个角相等,则称
中有两个角相等,则称![]() 是
是![]() 的“等心”.特别地,若这三个角都相等,则称
的“等心”.特别地,若这三个角都相等,则称![]() 是
是![]() 的“恒等心”.
的“恒等心”.
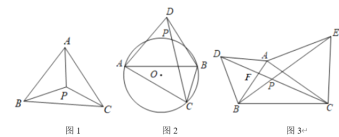
(1)在等边![]() 中,点
中,点![]() 是恒等心,
是恒等心,![]() ,则点
,则点![]() 到
到![]() 的距离是_______;
的距离是_______;
(2)如图2,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的外接圆外一点,连接
的外接圆外一点,连接![]() ,交
,交![]() 于点
于点![]() ,试判断
,试判断![]() 是不是
是不是![]() 的“等心”,并说明理由;
的“等心”,并说明理由;
(3)如图3,分别以锐角![]() 的边
的边![]() 、
、![]() 为边向外做等边
为边向外做等边![]() 和等边
和等边![]() ,
,![]() 和
和![]() 相交于点
相交于点![]() ,求证:点
,求证:点![]() 是
是![]() 的“恒等心”.
的“恒等心”.
查看答案和解析>>
科目:初中数学 来源: 题型:
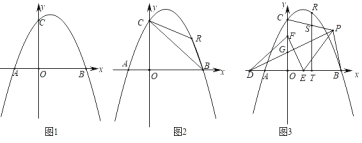
【题目】已知:在平面直角坐标系中,抛物线y=ax2﹣2ax+4(a<0)交x轴于点A、B,与y轴交于点C,AB=6.
(1)如图1,求抛物线的解析式;
(2)如图2,点R为第一象限的抛物线上一点,分别连接RB、RC,设△RBC的面积为s,点R的横坐标为t,求s与t的函数关系式;
(3)在(2)的条件下,如图3,点D在x轴的负半轴上,点F在y轴的正半轴上,点E为OB上一点,点P为第一象限内一点,连接PD、EF,PD交OC于点G,DG=EF,PD⊥EF,连接PE,∠PEF=2∠PDE,连接PB、PC,过点R作RT⊥OB于点T,交PC于点S,若点P在BT的垂直平分线上,OB﹣TS=![]() ,求点R的坐标.
,求点R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
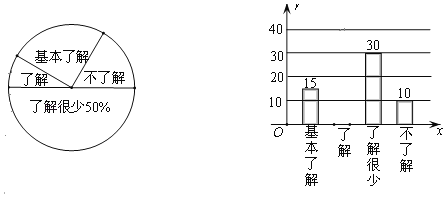
【题目】“食品安全”受到全社会的广泛关注,武汉市某中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 人,扇形统计图中“了解”部分所对应扇形的圆心角为 ;
(2)若从对食品安全知识达到“了解”程度的2个女生和2个男生中随机抽取2人参加食品安全知识竞赛,恰好抽到1个男生和1个女生的概率为 ;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
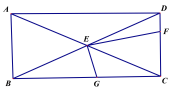
【题目】如图,AB∥CD,AD与BC相交于点E,AF平分∠BAD,交BC于点F,交CD的延长线于点G.

(1)若∠G=29°,求∠ADC的度数;
(2)若点F是BC的中点,求证:AB=AD+CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个芭蕾舞团演员的身高(单位:cm)如下表:
甲 | 164 | 164 | 165 | 165 | 166 | 166 | 167 | 167 |
乙 | 163 | 163 | 165 | 165 | 166 | 166 | 168 | 168 |
两组芭蕾舞团演员身高的方差较小的是______.(填“甲”或“乙”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,将直角的顶点E放在正方形ABCD的对角线AC上,使角的一边交CD于点F,另一边交CB或其延长线于点G,求![]() 的值;
的值;
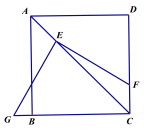
(2)如图,将(1)中的“正方形ABCD”改成“矩形ABCD”,其他条件不变.若AB=m,BC=n,试求![]() 的值;
的值;
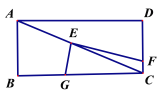
(3)如图,将直角顶点E放在矩形ABCD的对角线交点,EF、EG分别交CD与CB于点F、G,且EC平分∠FEG.若AB=2,BC=4,直接写出EG、EF 的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com