
【题目】如图1,点![]() 是
是![]() 的内部一点,连接
的内部一点,连接![]() 、
、![]() 和
和![]() ,如果
,如果![]() 、
、![]() 和
和![]() 中有两个角相等,则称
中有两个角相等,则称![]() 是
是![]() 的“等心”.特别地,若这三个角都相等,则称
的“等心”.特别地,若这三个角都相等,则称![]() 是
是![]() 的“恒等心”.
的“恒等心”.
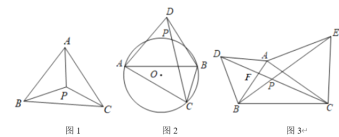
(1)在等边![]() 中,点
中,点![]() 是恒等心,
是恒等心,![]() ,则点
,则点![]() 到
到![]() 的距离是_______;
的距离是_______;
(2)如图2,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的外接圆外一点,连接
的外接圆外一点,连接![]() ,交
,交![]() 于点
于点![]() ,试判断
,试判断![]() 是不是
是不是![]() 的“等心”,并说明理由;
的“等心”,并说明理由;
(3)如图3,分别以锐角![]() 的边
的边![]() 、
、![]() 为边向外做等边
为边向外做等边![]() 和等边
和等边![]() ,
,![]() 和
和![]() 相交于点
相交于点![]() ,求证:点
,求证:点![]() 是
是![]() 的“恒等心”.
的“恒等心”.
【答案】(1)![]() ;(2)
;(2)![]() 是
是![]() 的“等心”,理由见解析;(3)证明见解析.
的“等心”,理由见解析;(3)证明见解析.
【解析】
(1)先根据“恒等心”的定义求出![]() ,再根据三角形全等的判定定理与性质得出
,再根据三角形全等的判定定理与性质得出![]() ,然后根据等腰三角形的性质可得
,然后根据等腰三角形的性质可得![]() ,最后解直角三角形即可得;
,最后解直角三角形即可得;
(2)先根据等腰三角形的性质可得![]() ,再根据圆周角定理可得
,再根据圆周角定理可得![]() ,从而可得
,从而可得![]() ,然后根据领补角的定义、等量代换可得
,然后根据领补角的定义、等量代换可得![]() ,最后根据圆内接四边形的性质可得
,最后根据圆内接四边形的性质可得![]() ,从而可得
,从而可得![]() ,由此即可得证;
,由此即可得证;
(3)如图(见解析),先根据三角形全等的判定定理可得![]() ,从而根据三角形全等的性质可得
,从而根据三角形全等的性质可得![]() ,再根据三角形的外角性质可得
,再根据三角形的外角性质可得![]() ,从而可得
,从而可得![]() ,然后根据相似三角形的判定与性质可得
,然后根据相似三角形的判定与性质可得![]() ,又根据相似三角形的判定与性质可得
,又根据相似三角形的判定与性质可得![]() ,最后根据角的和差可得出
,最后根据角的和差可得出![]() ,由此即可得证.
,由此即可得证.
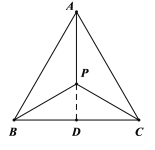
(1)如图,过点P作![]() 于点D
于点D
由“恒等心”的定义得:![]()
![]()
![]()
![]()
![]()
![]() 是等边三角形
是等边三角形
![]()
![]()
在![]() 和
和![]() 中,
中,
![]()
![]()
![]()
![]() (等腰三角形的三线合一)
(等腰三角形的三线合一)
在![]() 中,
中,![]() ,即
,即![]()
解得![]()
即点![]() 到
到![]() 的距离是2
的距离是2
故答案为:![]() ;
;
(2)如图,连接PA、PB
![]()
![]()
由圆周角定理得:![]()
![]()
又![]()
![]()
由圆内接四边形的性质可知,![]()
![]()
![]()
![]() 是
是![]() 的“等心”;
的“等心”;

(3)如图,连接![]()
![]() 和
和![]() 都是等边三角形
都是等边三角形
![]() ,
,![]() ,
,![]()
![]() ,即
,即![]()
在![]() 和
和![]() 中,
中,
![]()
![]()
![]()
![]()
![]()
![]()
在![]() 和
和![]() 中,
中,![]()
![]()
![]() ,即
,即![]()
在![]() 和
和![]() 中,
中,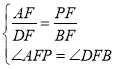
![]()
![]()
![]()
![]()
![]()
则点![]() 是
是![]() 的“恒等心”.
的“恒等心”.



科目:初中数学 来源: 题型:
【题目】某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西72°方向,距A船24海里的海域,C船位于A船的北偏东33°方向,同时又位于B船的北偏东78°方向.
(1)求∠ABC的度数;
(2)A船以每小时30海里的速度前去救援,问多长时间能到出事地点.(结果精确到0.01小时).
(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新型冠状病毒肺炎疫情发生后,全社会的积极参与疫情防控工作下,才有了我们的平安复学.为了能在复学前将一批防疫物资送达校园,某运输公司组织了甲、乙两种货车,已知甲种货车比乙种货车每辆车多装20箱防疫物资,且甲种货车装运900箱防疫物资所用车辆与乙种货车装运600箱防疫物资所用的车辆相等,求甲、乙两种货车每辆车可装多少箱防疫物资?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据规定,我市将垃圾分为了四类:可回收垃圾、餐厨垃圾、有害垃圾和其他垃圾.现有投放这四类垃圾的垃圾桶各1个,若将用不透明垃圾袋分类打包好的两袋不同垃圾随机投人进两个不同的垃圾桶,投放正确的概率是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于平面直角坐标系![]() 中的线段
中的线段![]() 和点
和点![]() ,在
,在![]() 中,当
中,当![]() 边上的高为2时,称
边上的高为2时,称![]() 为
为![]() 的“等高点”,称此时
的“等高点”,称此时![]() 为
为![]() 的“等高距离”.
的“等高距离”.
(1)若点![]() 的坐标为(1,2),点
的坐标为(1,2),点![]() 的坐标为(4,2),则在点
的坐标为(4,2),则在点![]() (1,0),
(1,0),![]() (
(![]() ,4),
,4),![]() (0,3)中,
(0,3)中,![]() 的“等高点”是点___;
的“等高点”是点___;
(2)若![]() (0,0),
(0,0),![]() =2,当
=2,当![]() 的“等高点”在
的“等高点”在![]() 轴正半轴上且“等高距离”最小时,点
轴正半轴上且“等高距离”最小时,点![]() 的坐标是__.
的坐标是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
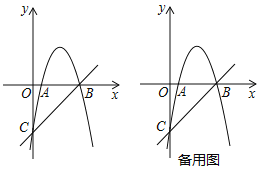
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() .直线
.直线![]() 经过点
经过点![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)过点![]() 的直线交直线
的直线交直线![]() 于点
于点![]() .
.
①当![]() 时,过抛物线上一动点
时,过抛物线上一动点![]() (不与点
(不与点![]() ,
,![]() 重合),作直线
重合),作直线![]() 的平行线交直线
的平行线交直线![]() 于点
于点![]() ,若以点
,若以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形,求点
为顶点的四边形是平行四边形,求点![]() 的横坐标;
的横坐标;
②连接![]() ,当直线
,当直线![]() 与直线
与直线![]() 的夹角等于
的夹角等于![]() 的
的![]() 倍时,请直接写出点
倍时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生开展义务植树活动,在活动结束后随机调查了40名学生每人植树的棵数,根据调查获取的样本数据,制作了条形统计图和扇形统计图.请根据相关信息,解答下列问题:
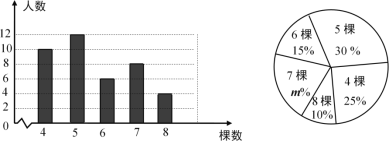
(1)扇形图中![]() 的值是_________;
的值是_________;
(2)求随机调查的40名学生每人植树棵数这组数据的平均数、众数和中位数;
(3)若本次活动九年级共有300名学生参加,估计植树超过6棵(不含6棵)的学生约有多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com