
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() .直线
.直线![]() 经过点
经过点![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)过点![]() 的直线交直线
的直线交直线![]() 于点
于点![]() .
.
①当![]() 时,过抛物线上一动点
时,过抛物线上一动点![]() (不与点
(不与点![]() ,
,![]() 重合),作直线
重合),作直线![]() 的平行线交直线
的平行线交直线![]() 于点
于点![]() ,若以点
,若以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形,求点
为顶点的四边形是平行四边形,求点![]() 的横坐标;
的横坐标;
②连接![]() ,当直线
,当直线![]() 与直线
与直线![]() 的夹角等于
的夹角等于![]() 的
的![]() 倍时,请直接写出点
倍时,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)①
;(2)①![]() 点的横坐标为
点的横坐标为![]() 或
或![]() 或
或![]() ;②点
;②点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)利用一次函数解析式确定C(0,-5),B(5,0),然后利用待定系数法求抛物线解析式;
(2)①先解方程-x2+6x-5=0得A(1,0),再判断△OCB为等腰直角三角形得到∠OBC=∠OCB=45°,则△AMB为等腰直角三角形,所以AM=2![]() ,接着根据平行四边形的性质得到PQ=AM=2
,接着根据平行四边形的性质得到PQ=AM=2![]() ,PQ⊥BC,作PD⊥x轴交直线BC于D,如图1,利用∠PDQ=45°得到PD=
,PQ⊥BC,作PD⊥x轴交直线BC于D,如图1,利用∠PDQ=45°得到PD=![]() PQ=4,设P(m,-m2+6m-5),则D(m,m-5),讨论:当P点在直线BC上方时,PD=-m2+6m-5-(m-5)=4;当P点在直线BC下方时,PD=m-5-(-m2+6m-5),然后分别解方程即可得到P点的横坐标;
PQ=4,设P(m,-m2+6m-5),则D(m,m-5),讨论:当P点在直线BC上方时,PD=-m2+6m-5-(m-5)=4;当P点在直线BC下方时,PD=m-5-(-m2+6m-5),然后分别解方程即可得到P点的横坐标;
②作AN⊥BC于N,NH⊥x轴于H,作AC的垂直平分线交BC于M1,交AC于E,如图2,利用等腰三角形的性质和三角形外角性质得到∠AM1B=2∠ACB,再确定N(3,-2),
AC的解析式为y=5x-5,E点坐标为(![]() ,-
,-![]() ),利用两直线垂直的问题可设直线EM1的解析式为y=-
),利用两直线垂直的问题可设直线EM1的解析式为y=-![]() x+b,把E(
x+b,把E(![]() ,-
,-![]() )代入求出b得到直线EM1的解析式为y=-
)代入求出b得到直线EM1的解析式为y=-![]() x-
x-![]() ,则解方程组
,则解方程组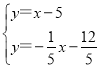 得M1点的坐标;作直线BC上作点M1关于N点的对称点M2,如图2,利用对称性得到∠AM2C=∠AM1B=2∠ACB,设M2(x,x-5),根据中点坐标公式得到3=
得M1点的坐标;作直线BC上作点M1关于N点的对称点M2,如图2,利用对称性得到∠AM2C=∠AM1B=2∠ACB,设M2(x,x-5),根据中点坐标公式得到3=![]() ,然后求出x即可得到M2的坐标,从而得到满足条件的点M的坐标.
,然后求出x即可得到M2的坐标,从而得到满足条件的点M的坐标.
(1)当![]() 时,
时,![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,解得
,解得![]() ,则
,则![]() ,
,
把![]() ,
,![]() 代入
代入![]()
得:![]() ,解得,
,解得,![]()
∴抛物线解析式为![]() ;
;
(2)①解方程![]() 得
得![]() ,
,![]() ,则
,则![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∵以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形,
为顶点的四边形是平行四边形,![]() ,
,
∴![]() ,
,![]() ,
,
作![]() 轴交直线
轴交直线![]() 于
于![]() ,如图1所示,则
,如图1所示,则![]()
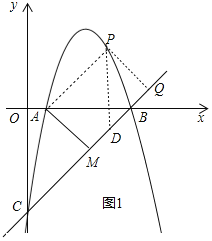
∴![]() ,
,
设![]() ,则
,则![]() ,
,
当![]() 点在直线
点在直线![]() 上方时,
上方时,
![]() ,解得
,解得![]() ,
,![]() ,
,
当![]() 点在直线
点在直线![]() 下方时
下方时
![]() ,
,
解得![]() ,
,![]() ,
,
综上所述,![]() 点的横坐标为
点的横坐标为![]() 或
或![]() 或
或![]() ;
;
②作![]() 于
于![]() ,
,![]() 轴于
轴于![]() ,作
,作![]() 的垂直平分线交
的垂直平分线交![]() 于
于![]() ,交
,交![]() 于
于![]() ,如图2,
,如图2,
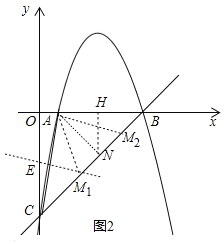
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
易得![]() 的解析式为
的解析式为![]() ,
,![]() 点坐标为
点坐标为![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
把![]() 代入得
代入得![]() ,解得
,解得![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
解方程组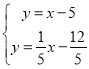 ,得
,得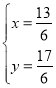 则
则![]() ;
;
作直线![]() 上作点
上作点![]() 关于
关于![]() 点的对称点
点的对称点![]() ,如图2,则
,如图2,则![]() ,
,
设![]() ,
,
∵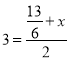 ,∴
,∴![]() ,∴
,∴![]() ,
,
综上所述,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】现有四个外观与质地完全相同的小球,小球上分别标有数字![]() .将四个小球放置于不透明的盒子中,摇匀后,甲从中随机抽取一个小球,记录数字后放回摇匀,乙再随机抽取一个.
.将四个小球放置于不透明的盒子中,摇匀后,甲从中随机抽取一个小球,记录数字后放回摇匀,乙再随机抽取一个.
(1)请用列表法或画树状图的方法,求两人抽取相同数字的概率.
(2)若两人抽取的数字和为![]() 的倍数,则甲获胜;若抽取的数字和为
的倍数,则甲获胜;若抽取的数字和为![]() 的倍数,则乙获胜,否则为平局.这个游戏公平吗?请用所学的概率的知识加以解释.
的倍数,则乙获胜,否则为平局.这个游戏公平吗?请用所学的概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为建设最美恩施,一旅游投资公司拟定在某景区用茶花和月季打造一片人工花海,经市场调查,购买![]() 株茶花与
株茶花与![]() 株月季的费用相同,购买
株月季的费用相同,购买![]() 株茶花与
株茶花与![]() 株月季共需
株月季共需![]() 元.
元.
(1)求茶花和月季的销售单价;
(2)该景区至少需要茶花月季共![]() 株,要求茶花比月季多
株,要求茶花比月季多![]() 株,但订购两种花的总费用不超过
株,但订购两种花的总费用不超过![]() 元,该旅游投资公司怎样购买所需总费用最低,最低费用是多少.
元,该旅游投资公司怎样购买所需总费用最低,最低费用是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC中,点D在边AC上,且AB2=ADAC.
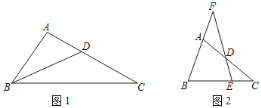
(1)如图1.求证:∠ABD=∠C.
(2)如图2.在边BC上截取BE=BD,ED、BA的延长线交于点F,求证:![]() .
.
(3)在 (2)的条件下,若AD=4,CD=5,cos∠BAC=![]() ,试直接写出△FBE的面积.
,试直接写出△FBE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用36000元购进甲、乙两种商品,销售完后共获利6000元.其中甲种商品每件进价120元,售价138元;乙种商品每件进价100元,售价120元.
(1)该商场购进甲、乙两种商品各多少件?
(2)商场第二次以原进价购进甲、乙两种商品,购进乙种商品的件数不变,而购进甲种商品的件数是第一次的2倍,甲种商品按原售价出售,而乙种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于8160元,乙种商品最低售价为每件多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校2400名学生到校上学的方式,在全校随机抽取了若干名学生进行问卷调査.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.将调査得到的结果绘制成如图所示的条形统计图和扇形统计图(均不完整)

(1)这次调查中,样本容量为 ,请补全条形统计图;
(2)小明在上学的路上要经过2个路口,每个路口都设有红、黄、绿三种信号灯,假设在各路口遇到三种信号灯的可能性相同,求小明在两个路口都遇到绿灯的概率.(请用“画树状图”或“列表”的方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
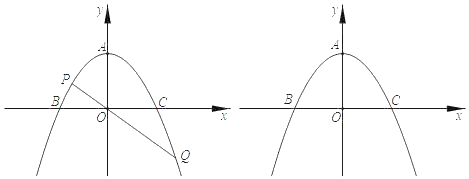
【题目】已知:如图,抛物线![]() 的顶点为A(0,2),与x轴交于B(﹣2,0)、C(2,0)两点.
的顶点为A(0,2),与x轴交于B(﹣2,0)、C(2,0)两点.
(1)求抛物线![]() 的函数表达式;
的函数表达式;
(2)设点P是抛物线y上的一个动点,连接PO并延长至点Q,使OQ=2OP.若点Q正好落在该抛物线上,求点P的坐标;
(3)设点P是抛物线y上的一个动点,连接PO并延长至点Q,使OQ=mOP(m为常数);
①证明点Q一定落在抛物线![]() 上;
上;
②设有一个边长为m+1的正方形(其中m>3),它的一组对边垂直于x轴,另一组对边垂直于y轴,并且该正方形四个顶点正好落在抛物线![]() 和
和![]() 组成的封闭图形上,求线段PQ被该正方形的两条边截得线段长最大时点Q的坐标.
组成的封闭图形上,求线段PQ被该正方形的两条边截得线段长最大时点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
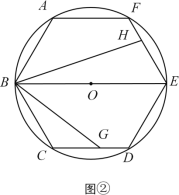
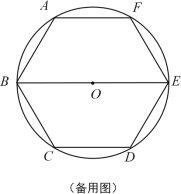
【题目】如图,已知圆O是正六边形ABCDEF外接圆,直径BE=8,点G、H分别在射线CD、EF上(点G不与点C、D重合),且∠GBH=60°,设CG=x,EH=y.
(1)如图①,当直线BG经过弧CD的中点Q时,求∠CBG的度数;
(2)如图②,当点G在边CD上时,试写出y关于x的函数关系式,并写出x的取值范围;
(3)联结AH、EG,如果△AFH与△DEG相似,求CG的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com