
【题目】已知:△ABC中,点D在边AC上,且AB2=ADAC.
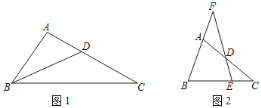
(1)如图1.求证:∠ABD=∠C.
(2)如图2.在边BC上截取BE=BD,ED、BA的延长线交于点F,求证:![]() .
.
(3)在 (2)的条件下,若AD=4,CD=5,cos∠BAC=![]() ,试直接写出△FBE的面积.
,试直接写出△FBE的面积.
【答案】(1)见解析;(2)见解析;(3)S△BEF=![]() .
.
【解析】
(1)根据两边成比例夹角相等两三角形相似证明△ABD∽△ACB即可解决问题.
(2)过点B作BG∥AC交FE的延长线于点G.证明△BDF≌△BEG(ASA),推出DF=EG,推出EF=GD,由BG∥AC推出![]() 可得答案 .
可得答案 .
(3)如图2中,过点B作BG∥AC交FE的延长线于点G,作CH⊥AB于H,FJ⊥BE于J.利用相似三角形的性质求出AB,再证明CA=CB,再利用相似三角形的性质求出BD,解直角三角形求出FJ即可解决问题.
(1)证明:如图1中,
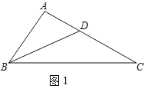
∵AB2=ADAC 即![]() ,
,
又∵∠A=∠A
∴△ABD∽△ACB,
∴∠ABD=∠C.
(2)解:过点B作BG∥AC交FE的延长线于点G.
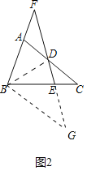
∵BG∥AC,
∴∠C=∠GBE,
∵∠ABD=∠C,
∴∠GBE=∠C=∠ABD,
∵BD=BE,
∴∠BDE=∠BED,
∴∠BDF=∠BEG,
∴△BDF≌△BEG(ASA),
∴DF=EG,
∴EF=GD,
∵BG∥AC,
∴![]() ,
,
即![]() .
.
(3)解:如图2中,过点B作BG∥AC交FE的延长线于点G,作CH⊥AB于H,FJ⊥BE于J.
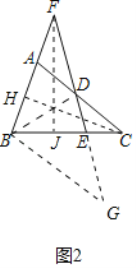
∵AB2=ADAC,AD=4.CD=5,
∴AB2=4×9,
∴AB=6,
在Rt△AHC中,∵cos∠CAH=![]() ,
,
∴AH=3,
∴BH=AH=3,
∵CH⊥AB,
∴CA=CB,
∴∠CAB=∠CBA,
∵AD∥BG,
∴![]() ,
,
![]() △BDF≌△BEG
△BDF≌△BEG
![]() FB=BG,
FB=BG,
∴AF=AD=4,
∴BF=AB+AF=6+4=10,
∵cos∠FBJ=cos∠BAC=![]() ,
,
∴BJ=![]() ,
,
∴FJ=![]() ,
,
∵△ABD∽△ACB,
∴![]() ,
,
∴![]() ,
,
∴BD=BE=6,
∴S△BEF=![]() BEFJ=
BEFJ=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 、
、![]() 、
、![]() 三点的坐标分别为
三点的坐标分别为![]() ,
,![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 上的一个动点,连接
上的一个动点,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() ,当点
,当点![]() 从
从![]() 运动到
运动到![]() 时,点
时,点![]() 随之运动,设点
随之运动,设点![]() 的坐标为
的坐标为![]() ,则
,则![]() 的取值范围是_____.
的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王电子产品专柜以20元/副的价格批发了某新款耳机,在试销的60天内整理出了销售数据如下
销售数据(第x天) | 售价(元) | 日销售量(副) |
1≤x<35 | x+30 | 100﹣2x |
35≤x≤60 | 70 | 100﹣2x |
(1)若试销阶段每天的利润为W元,求出W与x的函数关系式;
(2)请问在试销阶段的哪一天销售利润W可以达到最大值?最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区的三个景点![]() 在同一线路上,甲、乙两名游客从景点
在同一线路上,甲、乙两名游客从景点![]() 出发,甲步行到景点
出发,甲步行到景点![]() 乙乘景区观光车先到景点
乙乘景区观光车先到景点![]() 在
在![]() 处停留一段时间后,再步行到景点
处停留一段时间后,再步行到景点![]() .甲、乙两人离开景点
.甲、乙两人离开景点![]() 后的路程
后的路程![]() (米)关于时间
(米)关于时间![]() (分钟)的函数图象如图所示.根据以上信息回答下列问题:
(分钟)的函数图象如图所示.根据以上信息回答下列问题:
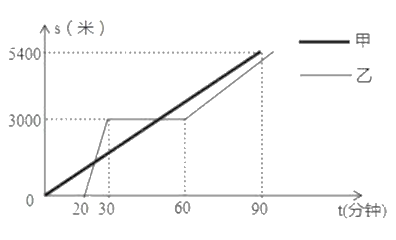
(1)乙出发后多长时间与甲相遇?
(2)若当甲到达景点![]() 时,乙与景点
时,乙与景点![]() 的路程为
的路程为![]() 米,则乙从景点
米,则乙从景点![]() 步行到景点
步行到景点![]() 的速度是多少?
的速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
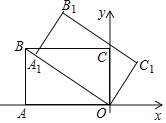
【题目】如图,平面直角坐标系中,矩形OABC的顶点A(﹣6,0),C(0,2![]() ).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
).将矩形OABC绕点O顺时针方向旋转,使点A恰好落在OB上的点A1处,则点B的对应点B1的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
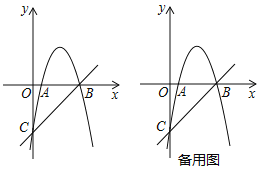
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() .直线
.直线![]() 经过点
经过点![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)过点![]() 的直线交直线
的直线交直线![]() 于点
于点![]() .
.
①当![]() 时,过抛物线上一动点
时,过抛物线上一动点![]() (不与点
(不与点![]() ,
,![]() 重合),作直线
重合),作直线![]() 的平行线交直线
的平行线交直线![]() 于点
于点![]() ,若以点
,若以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形,求点
为顶点的四边形是平行四边形,求点![]() 的横坐标;
的横坐标;
②连接![]() ,当直线
,当直线![]() 与直线
与直线![]() 的夹角等于
的夹角等于![]() 的
的![]() 倍时,请直接写出点
倍时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
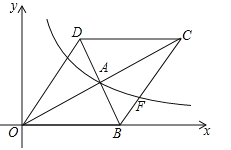
【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴上,反比例函数![]() (x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).
(x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).
(1)求反比例函数的表达式;
(2)求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】骆驼被称为“沙漠之舟”,它的体温随时间的变化而发生较大变化,其体温(![]() )与时间(小时)之间的关系如图1所示.
)与时间(小时)之间的关系如图1所示.

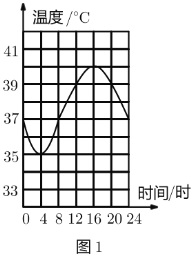
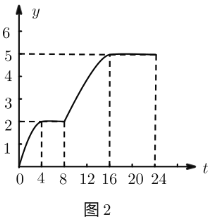
小清同学根据图1绘制了图2,则图2中的变量有可能表示的是( ).
A.骆驼在![]() 时刻的体温与0时体温的绝对差(即差的绝对值)
时刻的体温与0时体温的绝对差(即差的绝对值)
B.骆驼从0时到![]() 时刻之间的最高体温与当日最低体温的差
时刻之间的最高体温与当日最低体温的差
C.骆驼在![]() 时刻的体温与当日平均体温的绝对差
时刻的体温与当日平均体温的绝对差
D.骆驼从0时到![]() 时刻之间的体温最大值与最小值的差
时刻之间的体温最大值与最小值的差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com