
【题目】根据规定,我市将垃圾分为了四类:可回收垃圾、餐厨垃圾、有害垃圾和其他垃圾.现有投放这四类垃圾的垃圾桶各1个,若将用不透明垃圾袋分类打包好的两袋不同垃圾随机投人进两个不同的垃圾桶,投放正确的概率是________.

 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:初中数学 来源: 题型:
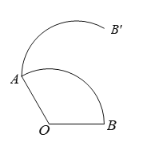
【题目】如图,将圆心角为120°的扇形AOB绕着点A按逆时针方向旋转一定的角度后,得到扇形AO′B′,使得点O′ 恰![]() 在上.
在上.
(1)求作点O′;(尺规作图,保留作图痕迹,不写作法和证明过程)
(2)连接AB、AB'、AO′,求证:AO′平分∠BAB′.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,二次函数y=﹣![]() x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
(1)填空:b= ,c= ;
(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;
(3)在x轴下方,该二次函数的图象上是否存在点M,使△PQM是以点P为直角顶点的等腰直角三角形?若存在,请求出运动时间t;若不存在,请说明理由;
(4)如图②,点N的坐标为(﹣![]() ,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标.
,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着时代的不断发展,新颖的网络购进逐渐融入到人们的生活中,“拼一拼”电商平台上提供了一种拼团购买方式,当拼团(单数不超过15单)成功后商家将会让利一定的额度给予顾客实惠.现在某商家准备出手一种每件成本25元/件的新产品,经市场调研发现,单价y(单位:元)、日销售量m(单位:件)与拼单数x(单位:单)之间存在着如表的数量关系:
拼单数x(单位:单) | 2 | 4 | 8 | 12 |
单价y(单位:元) | 34.50 | 34.00 | 33.00 | 32.00 |
日销售量m(单位:件) | 68 | 76 | 92 | 108 |
请根据以上提供的信息解决下列问题:
(1)请直接写出单价y和日销售量m分别与拼单数x之间的一次函数关系式;
(2)拼单数设置为多少单时的日销售利润最大,最大的销售利润是多少?
(3)在实际销售过程中,厂家希望能有更多的商品出售,因此对电商每销售一件商品厂家就给予电商补助a元(a≤2),那么电商在获得补助之日后日销售利润能够随单数x的增大而增大,那么a的取值范围是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】投石机是古代的大型攻城武器,是数学、工程、物理等复杂学科相互融合的应用(如图(1)).在我国《元史·亦思马因传》中对这种投石机就有过记载(如图(2)).
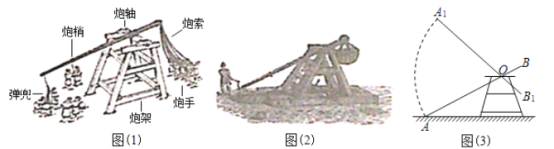
图(3)是图(1)中人工投石机的侧面示意图,炮架的横向支架均与地面相互平行,已知![]() 米,炮轴距地面4.5米,
米,炮轴距地面4.5米,![]()
![]() ,炮梢顶端点
,炮梢顶端点![]() 能到达水平地面,最高点能到达点
能到达水平地面,最高点能到达点![]() 处,且旋转的夹角
处,且旋转的夹角![]() (点
(点![]() ,
,![]() ,
,![]() ,
,![]() 在同一平面内),求点
在同一平面内),求点![]() 到水平地面的距离.(参考数据:
到水平地面的距离.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+(m﹣2)x+3(m+1)与x轴交于AB两点(A在B左侧),与y轴正半轴交于点C.
(1)当m≠﹣4时,说明这个二次函数的图象与x轴必有两个交点;
(2)若OAOB=6,求点C的坐标;
(3)在(2)的条件下,在x轴下方的抛物线上找一点P,使S△PAC的面积为15,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 是
是![]() 的内部一点,连接
的内部一点,连接![]() 、
、![]() 和
和![]() ,如果
,如果![]() 、
、![]() 和
和![]() 中有两个角相等,则称
中有两个角相等,则称![]() 是
是![]() 的“等心”.特别地,若这三个角都相等,则称
的“等心”.特别地,若这三个角都相等,则称![]() 是
是![]() 的“恒等心”.
的“恒等心”.
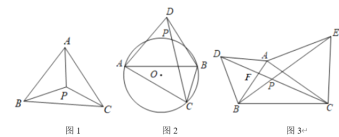
(1)在等边![]() 中,点
中,点![]() 是恒等心,
是恒等心,![]() ,则点
,则点![]() 到
到![]() 的距离是_______;
的距离是_______;
(2)如图2,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的外接圆外一点,连接
的外接圆外一点,连接![]() ,交
,交![]() 于点
于点![]() ,试判断
,试判断![]() 是不是
是不是![]() 的“等心”,并说明理由;
的“等心”,并说明理由;
(3)如图3,分别以锐角![]() 的边
的边![]() 、
、![]() 为边向外做等边
为边向外做等边![]() 和等边
和等边![]() ,
,![]() 和
和![]() 相交于点
相交于点![]() ,求证:点
,求证:点![]() 是
是![]() 的“恒等心”.
的“恒等心”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,抛物线y=ax2﹣2ax+4(a<0)交x轴于点A、B,与y轴交于点C,AB=6.
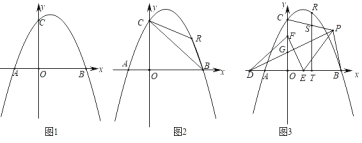
(1)如图1,求抛物线的解析式;
(2)如图2,点R为第一象限的抛物线上一点,分别连接RB、RC,设△RBC的面积为s,点R的横坐标为t,求s与t的函数关系式;
(3)在(2)的条件下,如图3,点D在x轴的负半轴上,点F在y轴的正半轴上,点E为OB上一点,点P为第一象限内一点,连接PD、EF,PD交OC于点G,DG=EF,PD⊥EF,连接PE,∠PEF=2∠PDE,连接PB、PC,过点R作RT⊥OB于点T,交PC于点S,若点P在BT的垂直平分线上,OB﹣TS=![]() ,求点R的坐标.
,求点R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个芭蕾舞团演员的身高(单位:cm)如下表:
甲 | 164 | 164 | 165 | 165 | 166 | 166 | 167 | 167 |
乙 | 163 | 163 | 165 | 165 | 166 | 166 | 168 | 168 |
两组芭蕾舞团演员身高的方差较小的是______.(填“甲”或“乙”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com