
【题目】投石机是古代的大型攻城武器,是数学、工程、物理等复杂学科相互融合的应用(如图(1)).在我国《元史·亦思马因传》中对这种投石机就有过记载(如图(2)).
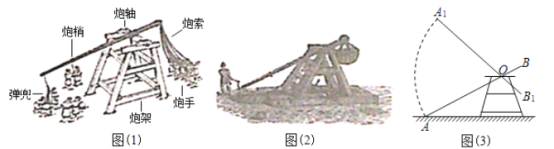
图(3)是图(1)中人工投石机的侧面示意图,炮架的横向支架均与地面相互平行,已知![]() 米,炮轴距地面4.5米,
米,炮轴距地面4.5米,![]()
![]() ,炮梢顶端点
,炮梢顶端点![]() 能到达水平地面,最高点能到达点
能到达水平地面,最高点能到达点![]() 处,且旋转的夹角
处,且旋转的夹角![]() (点
(点![]() ,
,![]() ,
,![]() ,
,![]() 在同一平面内),求点
在同一平面内),求点![]() 到水平地面的距离.(参考数据:
到水平地面的距离.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
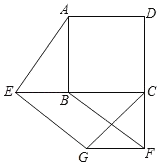
【题目】如图,E,F分别是正方形ABCD的边CB,DC延长线上的点,且BE=CF,过点E作EG∥BF,交正方形外角的平分线CG于点G,连接GF.
(1)求∠AEG的度数;
(2)求证:四边形BEGF是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明与小亮两个人打算骑共享单车骑行出游,两人打开手机APP进行选择,已知附近共有3种品牌的5辆车,其中A品牌与B品牌各有2辆,C品牌有1辆,手机上无法识别品牌,且有人选中车后其他人无法再选.
(1)若小明首先选择,则小明选中A品牌单车的概率为 ;
(2)求小明和小亮选中同一品牌单车的概率.(请用“画树状图”或“列表”的方法给出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新型冠状病毒肺炎疫情发生后,全社会的积极参与疫情防控工作下,才有了我们的平安复学.为了能在复学前将一批防疫物资送达校园,某运输公司组织了甲、乙两种货车,已知甲种货车比乙种货车每辆车多装20箱防疫物资,且甲种货车装运900箱防疫物资所用车辆与乙种货车装运600箱防疫物资所用的车辆相等,求甲、乙两种货车每辆车可装多少箱防疫物资?
查看答案和解析>>
科目:初中数学 来源: 题型:
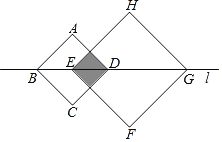
【题目】如图,正方形ABCD和正方形EFGH的对角线BD,EG都在直线l上,将正方形ABCD沿着直线l从点D与点E重合开始向右平移,直到点B与点G重合为止,设点D平移的距离为x,![]() ,
,![]() ,两个正方形重合部分的面积为S,则S关于x的函数图象大致为( )
,两个正方形重合部分的面积为S,则S关于x的函数图象大致为( )
A.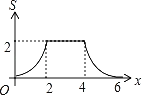 B.
B.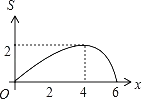
C.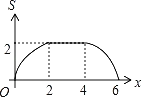 D.
D.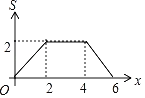
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据规定,我市将垃圾分为了四类:可回收垃圾、餐厨垃圾、有害垃圾和其他垃圾.现有投放这四类垃圾的垃圾桶各1个,若将用不透明垃圾袋分类打包好的两袋不同垃圾随机投人进两个不同的垃圾桶,投放正确的概率是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() .直线
.直线![]() 经过点
经过点![]() ,
,![]() .
.
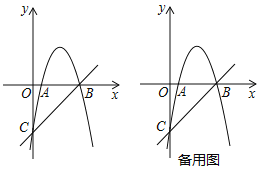
(1)求抛物线的解析式;
(2)过点![]() 的直线交直线
的直线交直线![]() 于点
于点![]() .
.
①当![]() 时,过抛物线上一动点
时,过抛物线上一动点![]() (不与点
(不与点![]() ,
,![]() 重合),作直线
重合),作直线![]() 的平行线交直线
的平行线交直线![]() 于点
于点![]() ,若以点
,若以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形,求点
为顶点的四边形是平行四边形,求点![]() 的横坐标;
的横坐标;
②连接![]() ,当直线
,当直线![]() 与直线
与直线![]() 的夹角等于
的夹角等于![]() 的
的![]() 倍时,请直接写出点
倍时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=![]() (m为常数,且n≠0)的图象交于点A(﹣3,1)、B(1,n).
(m为常数,且n≠0)的图象交于点A(﹣3,1)、B(1,n).
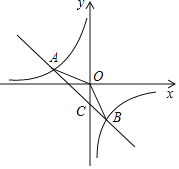
(1)求反比例函数和一次函数的解析式;
(2)连结0A、OB,求△AOB的面积;
(3)直接写出当y1<y2<0时,自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com