
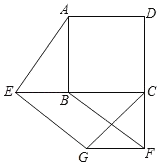
【题目】如图,E,F分别是正方形ABCD的边CB,DC延长线上的点,且BE=CF,过点E作EG∥BF,交正方形外角的平分线CG于点G,连接GF.
(1)求∠AEG的度数;
(2)求证:四边形BEGF是平行四边形.
【答案】(1)90°;(2)证明见解析.
【解析】
(1)由SAS证明△ABE≌△BCF得出AE=BF,∠BAE=∠CBF,由平行线的性质得出∠CBF=∠CEG,证出AE⊥EG,即可得出结论;
(2)延长AB至点P,使BP=BE,连接EP,则AP=CE,∠EBP=90°,证明△APE≌△ECG得出AE=EG,证出EG=BF,即可得出结论.
证明:(1)∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCD=90°,
∴∠ABE=∠BCF=90°,
在△ABE和△BCF中,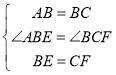
∴△ABE≌△BCF(SAS),
∴AE=BF,∠BAE=∠CBF,
∵EG∥BF,
∴∠CBF=∠CEG,
∵∠BAE+∠BEA=90°,
∴∠CEG+∠BEA=90°,
∴AE⊥EG,
∴∠AEG的度数为90°;
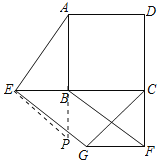
(2)延长AB至点P,使BP=BE,连接EP,如图所示:
则AP=CE,∠EBP=90°,
∴∠P=45°,
∵CG为正方形ABCD外角的平分线,
∴∠ECG=45°,
∴∠P=∠ECG,
由(1)得∠BAE=∠CEG,
在△APE和△ECG中,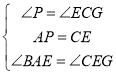
∴△APE≌△ECG(ASA),
∴AE=EG,
∵AE=BF,
∴EG=BF,
∵EG∥BF,
∴四边形BEGF是平行四边形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为了研究一种新药的疗效,选100名患者随机分成两组,每组各50名,一组服药,另一组不服药,12周后,记录了两组患者的生理指标![]() 和
和![]() 的数据,并制成下图,其中“*”表示服药者,“+”表示未服药者;
的数据,并制成下图,其中“*”表示服药者,“+”表示未服药者;
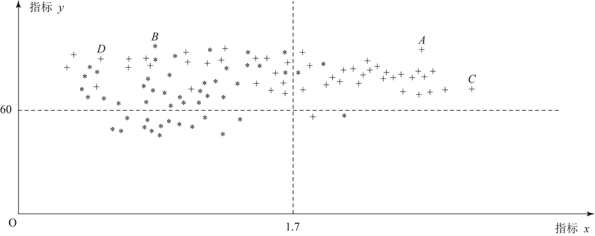
同时记录了服药患者在4周、8周、12周后的指标z的改善情况,并绘制成条形统计图.

根据以上信息,回答下列问题:
(1)从服药的50名患者中随机选出一人,求此人指标![]() 的值大于1.7的概率;
的值大于1.7的概率;
(2)设这100名患者中服药者指标![]() 数据的方差为
数据的方差为![]() ,未服药者指标
,未服药者指标![]() 数据的方差为
数据的方差为![]() ,则
,则![]()
![]() ;(填“>”、“=”或“<” )
;(填“>”、“=”或“<” )
(3)对于指标z的改善情况,下列推断合理的是 .
①服药4周后,超过一半的患者指标z没有改善,说明此药对指标z没有太大作用;
②在服药的12周内,随着服药时间的增长,对指标z的改善效果越来越明显.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解七、八年级学生一分钟跳绳情况,从这两个年级随机抽取![]() 名学生进行测试,并对测试成绩(一分钟跳绳次数)进行整理、描述和分析,下面给出了部分信息:
名学生进行测试,并对测试成绩(一分钟跳绳次数)进行整理、描述和分析,下面给出了部分信息:
七年级学生一分钟跳绳成绩频数分布直方图
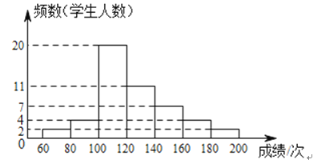
七、八年级学生一分钟跳绳成绩分析表

七年级学生一分钟跳绳成绩(数据分![]() 组:
组:![]() )在
)在![]() 这一组的是:
这一组的是:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
根据以上信息,回答下列问题:
![]() 表中
表中![]() ;
;
![]() 在这次测试中,七年级甲同学的成绩
在这次测试中,七年级甲同学的成绩![]() 次,八年级乙同学的成绩
次,八年级乙同学的成绩![]() ,他们的测试成绩,在各自年级所抽取的
,他们的测试成绩,在各自年级所抽取的![]() 名同学中,排名更靠前的是 (填“甲”或“乙”),理由是 .
名同学中,排名更靠前的是 (填“甲”或“乙”),理由是 .
![]() 该校七年级共有
该校七年级共有![]() 名学生,估计一分钟跳绳不低于
名学生,估计一分钟跳绳不低于![]() 次的有多少人?
次的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
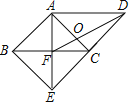
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,过点
,过点![]() 作边
作边![]() 的垂线
的垂线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,点
,点![]() 是垂足,连接
是垂足,连接![]() 、
、![]() ,
,![]() 交
交![]() 于点
于点![]() .则下列结论:①四边形
.则下列结论:①四边形![]() 是正方形;②
是正方形;②![]() ;③
;③![]() ;④
;④![]() ,正确的个数是( )
,正确的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
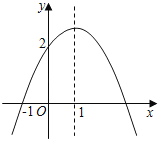
【题目】如图,抛物线y=ax2+bx+c经过点(﹣1,0),与y轴交于(0,2),抛物线的对称轴为直线x=1,则下列结论中:①a+c=b;②方程ax2+bx+c=0的解为﹣1和3;③2a+b=0;④c﹣a>2,其中正确的结论有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
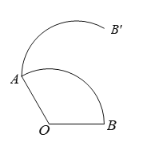
【题目】如图,将圆心角为120°的扇形AOB绕着点A按逆时针方向旋转一定的角度后,得到扇形AO′B′,使得点O′ 恰![]() 在上.
在上.
(1)求作点O′;(尺规作图,保留作图痕迹,不写作法和证明过程)
(2)连接AB、AB'、AO′,求证:AO′平分∠BAB′.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接2022年冬奥会,鼓励更多的大学生参与到志愿服务中,甲、乙两所学校组织了志愿服务团队选拔活动,经过初选,两所学校各有300名学生进入综合素质展示环节,为了了解这些学生的整体情况,从两校进入综合素质展示环节的学生中分别随机抽取了50名学生的综合素质展示成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
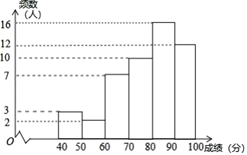
a.甲学校学生成绩的频数分布直方图如图(数据分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ).
).
b.甲学校学生成绩在![]() 这一组是:
这一组是:
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
c.乙学校学生成绩的平均数、中位数、众数、优秀率(85分及以上为优秀)如下:
平均数 | 中位数 | 众数 | 优秀率 |
83.3 | 84 | 78 | 46% |
根据以上信息,回答下列问题:
(1)甲学校学生![]() ,乙学校学生
,乙学校学生![]() 的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“
的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是________(填“![]() ”或“
”或“![]() ”);
”);
(2)根据上述信息,推断________学校综合素质展示的水平更高,理由为:__________________________
(至少从两个不同的角度说明推断的合理性).
(3)若每所学校综合素质展示的前120名学生将被选入志愿服务团队,预估甲学校分数至少达到________分的学生才可以入选.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】投石机是古代的大型攻城武器,是数学、工程、物理等复杂学科相互融合的应用(如图(1)).在我国《元史·亦思马因传》中对这种投石机就有过记载(如图(2)).
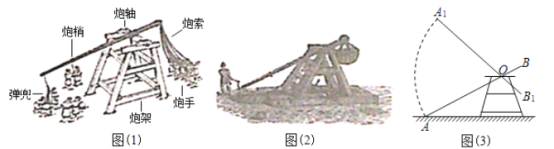
图(3)是图(1)中人工投石机的侧面示意图,炮架的横向支架均与地面相互平行,已知![]() 米,炮轴距地面4.5米,
米,炮轴距地面4.5米,![]()
![]() ,炮梢顶端点
,炮梢顶端点![]() 能到达水平地面,最高点能到达点
能到达水平地面,最高点能到达点![]() 处,且旋转的夹角
处,且旋转的夹角![]() (点
(点![]() ,
,![]() ,
,![]() ,
,![]() 在同一平面内),求点
在同一平面内),求点![]() 到水平地面的距离.(参考数据:
到水平地面的距离.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com