
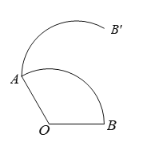
【题目】如图,将圆心角为120°的扇形AOB绕着点A按逆时针方向旋转一定的角度后,得到扇形AO′B′,使得点O′ 恰![]() 在上.
在上.
(1)求作点O′;(尺规作图,保留作图痕迹,不写作法和证明过程)
(2)连接AB、AB'、AO′,求证:AO′平分∠BAB′.
科目:初中数学 来源: 题型:
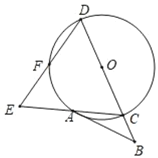
【题目】如图,AB与⊙O相切于点A,OB及其延长线交⊙O于C、D两点,F为劣弧AD上一点,且满足∠FDC=2∠CAB,延长DF交CA的延长线于点E.
(1)求证:DE=DC;
(2)若tan∠E=2,BC=1,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P为△ABC边上一动点,沿着A→C→B的路径行进,点P作PD⊥AB,垂足为D,设AD=x,△APD的面积为y,图2是y关于x的函数图象,则依据图中的数量关系计算△ACB的周长为( )
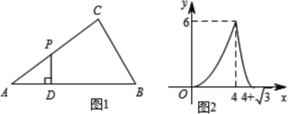

A.![]() B.15C.
B.15C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
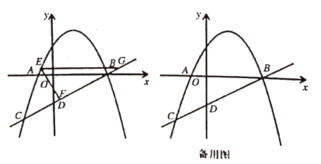
【题目】如图,二次函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() 为二次函数图象上任一点.
为二次函数图象上任一点.
![]() 求这个二次函数的解析式;
求这个二次函数的解析式;
![]() 若点
若点![]() 在直线
在直线![]() 的上方,过
的上方,过![]() 分别作
分别作![]() 和
和![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于不同的两点
于不同的两点![]() (
(![]() 在
在![]() 的左侧),求
的左侧),求![]() 周长的最大值;
周长的最大值;
![]() 是否存在点
是否存在点![]() 使得
使得![]() 是以
是以![]() 为直角边的直角三角形?如果存在,直接写出点
为直角边的直角三角形?如果存在,直接写出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
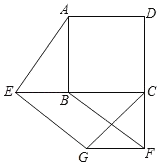
【题目】如图,E,F分别是正方形ABCD的边CB,DC延长线上的点,且BE=CF,过点E作EG∥BF,交正方形外角的平分线CG于点G,连接GF.
(1)求∠AEG的度数;
(2)求证:四边形BEGF是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2-2ax+c与x轴分别交于点A、B(点B在点A的右侧),与y轴交于点C,连接BC,点(![]() ,
,![]() a-3)在抛物线上.
a-3)在抛物线上.
(1)求c的值;
(2)已知点D与C关于原点O对称,作射线BD交抛物线于点E,若BD=DE,①求抛物线所对应的函数表达式 ;②过点B作BF⊥BC交抛物线的对称轴于点F,以点C为圆心,以![]() 的长为半径作⊙C,点T为⊙C上的一个动点,求
的长为半径作⊙C,点T为⊙C上的一个动点,求![]() TB+TF的最小值.
TB+TF的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某海域有A、B、C三艘船正在捕鱼作业,C船突然出现故障,向A、B两船发出紧急求救信号,此时B船位于A船的北偏西72°方向,距A船24海里的海域,C船位于A船的北偏东33°方向,同时又位于B船的北偏东78°方向.
(1)求∠ABC的度数;
(2)A船以每小时30海里的速度前去救援,问多长时间能到出事地点.(结果精确到0.01小时).
(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
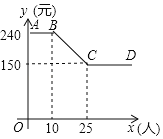
【题目】某公司组织员工到附近的景点旅游,根据旅行社提供的收费方案,绘制了如图所示的图象,图中折线ABCD表示人均收费y(元)与参加旅游的人数x(人)之间的函数关系.
(1)当参加旅游的人数不超过10人时,人均收费为 元;
(2)如果该公司支付给旅行社3600元,那么参加这次旅游的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据规定,我市将垃圾分为了四类:可回收垃圾、餐厨垃圾、有害垃圾和其他垃圾.现有投放这四类垃圾的垃圾桶各1个,若将用不透明垃圾袋分类打包好的两袋不同垃圾随机投人进两个不同的垃圾桶,投放正确的概率是________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com