
【题目】如图1,点P为△ABC边上一动点,沿着A→C→B的路径行进,点P作PD⊥AB,垂足为D,设AD=x,△APD的面积为y,图2是y关于x的函数图象,则依据图中的数量关系计算△ACB的周长为( )
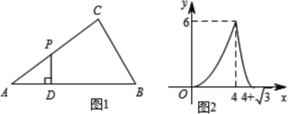

A.![]() B.15C.
B.15C.![]() D.
D.![]()
【答案】C
【解析】
根据函数图象得出拐点处坐标为(4,6),结合图3得出当点P运动到C点时,y有最大值6,从而计算出CD的值,勾股定理求出AC,根据当点D运动到B点时,函数值为0,求出AB的值,从而求出BD的值,利用锐角三角函数求出BC即可解答.
由图像可知函数图像的拐点处坐标为(4,6),
结合图3可知,当点P运动到C点时,y有最大值6,
可知:y=![]() AD·CD,代入数据得CD=3,
AD·CD,代入数据得CD=3,
在Rt△ADC中,AC=![]() =5,
=5,
当点D运动到B点时,函数值为0,故AB=![]() ,
,
∴BD=4+![]() -4=
-4=![]() ,
,
在Rt△BDC中,CD=3,BD=![]() ,tanB=
,tanB=![]() ,
,
得∠B=60°,由BD=BC·cos60°,得BC=![]() ,
,
∴△ABC的周长为:5+![]() +4 +
+4 +![]() =
= ![]() .
.
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于![]() BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若AD=AC,∠A=80°,则∠ACB的度数为( )
BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若AD=AC,∠A=80°,则∠ACB的度数为( )
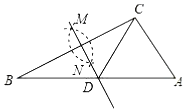
A.65°B.70°C.75°D.80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中(如图),已知点A在x轴的正半轴上,且与原点的距离为3,抛物线y=ax2﹣4ax+3(a≠0)经过点A,其顶点为C,直线y=1与y轴交于点B,与抛物线交于点D(在其对称轴右侧),联结BC、CD.
(1)求抛物线的表达式及点C的坐标;
(2)点P是y轴的负半轴上的一点,如果△PBC与△BCD相似,且相似比不为1,求点P的坐标;
(3)将∠CBD绕着点B逆时针方向旋转,使射线BC经过点A,另一边与抛物线交于点E(点E在对称轴的右侧),求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F.
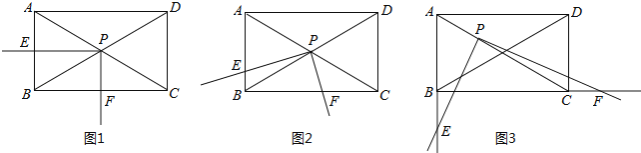
(1)当PE⊥AB,PF⊥BC时,如图1,则![]() 的值为 ;
的值为 ;
(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求![]() 的值;
的值;
(3)在(2)的基础上继续旋转,当60°<α<90°,且使AP:PC=1:2时,如图3,![]() 的值是否变化?证明你的结论.
的值是否变化?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加西部博览会,资阳市计划印制一批宣传册.该宣传册每本共10页,由A、B两种彩页构成.已知A种彩页制版费300元/张,B种彩页制版费200元/张,共计2400元.(注:彩页制版费与印数无关)
(1)每本宣传册A、B两种彩页各有多少张?
(2)据了解,A种彩页印刷费2.5元/张,B种彩页印刷费1.5元/张,这批宣传册的制版费与印刷费的和不超过30900元.如果按到资阳展台处的参观者人手一册发放宣传册,预计最多能发给多少位参观者?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接体育理化加试,九(2)班同学到某体育用品商店采购训练用球,已知购买3个A品牌足球和2个B品牌足球需付210元;购买2个A品牌足球和1个B品牌足球需付费130元.(优惠措施见海报)

(1)求A,B两品牌足球的单价各为多少元;
(2)为享受优惠,同学们决定购买一次性购买足球60个,若要求A品牌足球的数量不低于B品牌足球数量的3倍,请你设计一种付费最少的方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() (k≠0)的图像与一次函数y=-x+b的图像在第一象限交于A、B两点,BC⊥x轴于点C,若△OBC的面积为2,且A点的纵坐标为4,B点的纵坐标为1.
(k≠0)的图像与一次函数y=-x+b的图像在第一象限交于A、B两点,BC⊥x轴于点C,若△OBC的面积为2,且A点的纵坐标为4,B点的纵坐标为1.
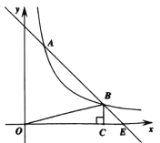
(1)求反比例函数、一次函数的表达式及直线AB与x轴交点E的坐标;
(2)已知点D(t,0)(t>0),过点D作垂直于x轴的直线,在第一象限内与一次函数y=-x+b的图像相交于点P,与反比函数![]() 上的图像相交于点Q,若点P位于点Q的上方,请结合函数图像直接写出此时t的取值范围.
上的图像相交于点Q,若点P位于点Q的上方,请结合函数图像直接写出此时t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
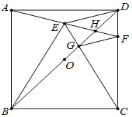
【题目】如图,正方形ABCD中,O为BD中点,以BC为边向正方形内作等边△BCE,连接AE并延长交CD于F,连接BD分别交CE、AF于G、H,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() :
:![]() ,其中正确的是__________.
,其中正确的是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,作出如图所示的统计图和统计表.请根据图表信息,解答下列问题:
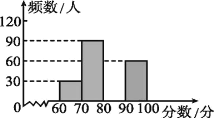

(1)在表中:m= ,n= ;在图中补全频数分布直方图;
(2)小明的成绩是所有被抽查学生成绩的中位数,据此推断他的成绩在 组;
(3)4个小组每组推荐1人,然后从4人中随机抽取2人参加颁奖典礼,恰好抽中A、C两组学生的概率是多少?请用列表法或画树状图法说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com