
【题目】为了解某市中学生参加“科普知识”竞赛成绩的情况,随机抽查了部分参赛学生的成绩,作出如图所示的统计图和统计表.请根据图表信息,解答下列问题:
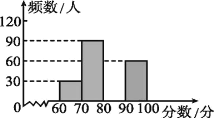

(1)在表中:m= ,n= ;在图中补全频数分布直方图;
(2)小明的成绩是所有被抽查学生成绩的中位数,据此推断他的成绩在 组;
(3)4个小组每组推荐1人,然后从4人中随机抽取2人参加颁奖典礼,恰好抽中A、C两组学生的概率是多少?请用列表法或画树状图法说明.
【答案】(1) m=120,n=0.3,补全频数分布直方图如图见解析;(2) C;(3)抽中A,C两组学生的概率为![]() .
.
【解析】
(1)先根据A组频数及其频率求得总人数,再根据频率=频数÷总人数可得m、n的值
(2)根据中位数的定义即可求解
(3)画树状图
(1)∵本次调查的总人数为30÷0.1=300(人),
∴m=300×0.4=120,n=90÷300=0.3,
补全频数分布直方图如图.

(2)由于共有300个数据,其中位数为第150,151个数据的平均数,而第150,151个数据均落在C组,
∴据此推断小明的成绩在C组,故答案为C.
(3)画树状图如下:

由树状图可知,共有12种等可能的结果,其中抽中A,C两组学生的有2种结果,∴抽中A,C两组学生的概率为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,点P为△ABC边上一动点,沿着A→C→B的路径行进,点P作PD⊥AB,垂足为D,设AD=x,△APD的面积为y,图2是y关于x的函数图象,则依据图中的数量关系计算△ACB的周长为( )
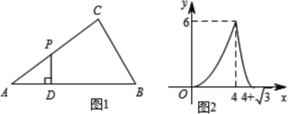

A.![]() B.15C.
B.15C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() 于
于![]() ,交
,交![]() 轴于点
轴于点![]()
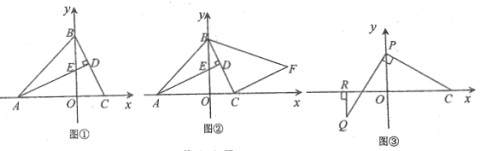
(1)如图①,求点![]() 的坐标;
的坐标;
(2)如图②:将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 后得线段
后得线段![]() ,连接
,连接![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图③, 点![]() 为
为![]() 轴正半轴上一动点, 点
轴正半轴上一动点, 点![]() 在第二象限内,
在第二象限内,![]() 于
于![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 垂直
垂直![]() 轴于点
轴于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
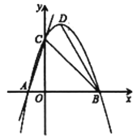
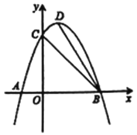
【题目】如图,一条抛物线与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() 为抛物线的顶点,点
为抛物线的顶点,点![]() 在
在![]() 轴上.
轴上.
(1)求抛物线解析式;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)过点![]() 作直线
作直线![]() 交抛物线于
交抛物线于![]() ,是否存在以点
,是否存在以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形?若存在,请求出点
为顶点的四边形是平行四边形?若存在,请求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(4)坐标平面内一点![]() 到点
到点![]() 的距离为1个单位,求
的距离为1个单位,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题呈现
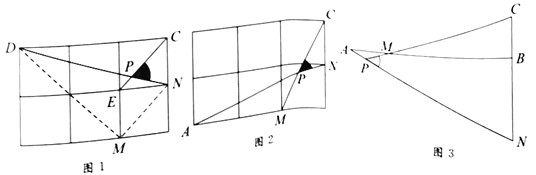
如图1,在边长为1的正方形网格中,连接格点![]() 、
、![]() 和
和![]() 、
、![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的值.
的值.
方法归纳
求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中![]() 不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题.比如连接格点
不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题.比如连接格点![]() 、
、![]() ,可得
,可得![]() ,则
,则![]() ,连接
,连接![]() ,那么
,那么![]() 就变换到中
就变换到中![]() .
.
问题解决
(1)直接写出图1中![]() 的值为_________;
的值为_________;
(2)如图2,在边长为1的正方形网格中,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的值;
的值;
思维拓展
(3)如图3,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() 交
交![]() 的延长线于点
的延长线于点![]() ,用上述方法构造网格求
,用上述方法构造网格求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
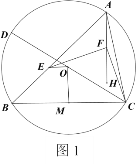
【题目】如图1,设![]() 是一个锐角三角形,且
是一个锐角三角形,且![]() ,
,![]() 为其外接圆,
为其外接圆,![]() 分别为其外心和垂心,
分别为其外心和垂心,![]() 为圆
为圆![]() 直径,
直径,![]() 为线段
为线段![]() 上一动点且满足
上一动点且满足![]() .
.
(1)证明:![]() 为
为![]() 中点;
中点;
(2)过![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,若
,若![]() 为
为![]() 的中点,证明:
的中点,证明: ![]() ;
;
(3)直线![]() 与圆
与圆![]() 的另一交点为
的另一交点为![]() (如图2),以
(如图2),以![]() 为直径的圆与圆
为直径的圆与圆![]() 的另一交点为
的另一交点为![]() .证明:若
.证明:若![]() 三线共点,则
三线共点,则![]() ;反之也成立.
;反之也成立.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“元旦大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有3张相同的卡片,卡片上分别标有“10元”、“20元”和“30元”的字样,规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里摸出一张卡片,记下钱数后放回,再从中摸出一张卡片.商场根据两张卡片所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客最多可得到 元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于40元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
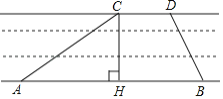
【题目】京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A、B和点C、D,先用卷尺量得AB=160m,CD=40m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com