
����Ŀ��Ϊ��ӭ�������������ԣ��ţ�2����ͬѧ��ij������Ʒ�̵�ɹ�ѵ��������֪����3��AƷ�������2��BƷ�������踶210Ԫ������2��AƷ�������1��BƷ�������踶��130Ԫ�����Żݴ�ʩ��������

��1����A��B��Ʒ������ĵ��۸�Ϊ����Ԫ��
��2��Ϊ�����Żݣ�ͬѧ�Ǿ�������һ���Թ�������60������Ҫ��AƷ�����������������BƷ������������3�����������һ�ָ������ٵķ�������˵�����ɣ�
���𰸡���1��AƷ������ĵ���Ϊ50Ԫ��BƷ������ĵ���Ϊ30Ԫ����2������AƷ������45����BƷ������15���������٣����ٷ���Ϊ2250Ԫ�����ɼ�������
��������
��1����AƷ������ĵ���ΪxԪ��BƷ������ĵ���ΪyԪ�����ݹ���3��AƷ�������2��BƷ�������踶210Ԫ������2��AƷ�������1��BƷ�������踶��130Ԫ�з��������ɵã�
��2���蹺��AƷ������Ϊa��������BƷ������Ϊ��60��a����������AƷ�����������������BƷ������������3����һԪһ�β���ʽ��⣬Ȼ����������ʾ�������ܷ���W��a�ĺ�����ϵʽ��Ȼ�����һ�κ���ͼ�����ʷ�����ֵ��
�⣺��1����AƷ������ĵ���ΪxԪ��BƷ������ĵ���ΪyԪ����������ã�![]() �����
�����![]() ����AƷ������ĵ���Ϊ50Ԫ��BƷ������ĵ���Ϊ30Ԫ��
����AƷ������ĵ���Ϊ50Ԫ��BƷ������ĵ���Ϊ30Ԫ��
��2���蹺��AƷ������Ϊa��������BƷ������Ϊ��60��a��������������ã�
![]() �����
�����![]() ����AƷ���������8�ۣ�BƷ������ԭ�ۣ�
����AƷ���������8�ۣ�BƷ������ԭ�ۣ�
�蹺��A��B��Ʒ��������ܷ���ΪWԪ��
��W��0��8��50a+30��60��a����10a+1800��
��k��10��0����W��x�����������
�൱a��45ʱ���������٣����ٷ���Ϊ��10��45+1800��2250��Ԫ����
�𣺹���AƷ������45����BƷ������15���������٣����ٷ���Ϊ2250Ԫ��


 ѧ���������ν��Ͼ���ѧ������ϵ�д�
ѧ���������ν��Ͼ���ѧ������ϵ�д� Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
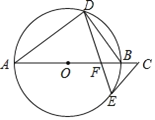
����Ŀ����ͼ��AB�ǡ�O��ֱ������D��E�ڡ�O�ϣ���A=2��BDE����C��AB���ӳ����ϣ���C=��ABD��
��1����֤��CE�ǡ�O�����ߣ�
��2������O�İ뾶��Ϊ5��BF=2����EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������IJ�����װ��4������1��2��3��4��С�����ǵ���״����С���ʵ���ȫ��ͬ��С��Ӳ��������ȡ��һ��С��������Ϊx��С����ʣ�µ�3��С�������ȡ��һ��С��������Ϊy������ȷ���˵�Q�����꣨x��y����
��1������״ͼ���б���д����Q���п��ܵ����ꣻ
��2�����Q��x��y���ں���y=��x+5ͼ���ϵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�е�A�͡�B�͡�C�;���ֽƬ�ֱ����3�������У����ӵ���״����С���ʵض���ͬ���ٽ���3������װ��һֻ�����Ĵ����У�
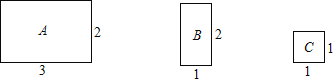
��1�����Ⱥ��������1�����ӣ��������ĺ�������![]() �;���ֽƬ�ĸ��ʣ�
�;���ֽƬ�ĸ��ʣ�
��2�����Ⱥ��ȴ�������1�����ӣ����Żأ����ٴ����µ���������������һ�����ӣ���2�������ĺ��ӵ�ֽƬ��ƴ��һ���¾��εĸ��ʣ����ص���϶ƴ�ӣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����PΪ��ABC����һ���㣬����A��C��B��·���н�����P��PD��AB������ΪD����AD��x����APD�����Ϊy��ͼ2��y����x�ĺ���ͼ��������ͼ�е�������ϵ������ACB���ܳ�Ϊ�� ��
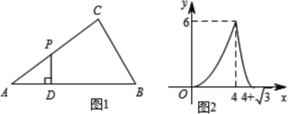

A.![]() B.15C.
B.15C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
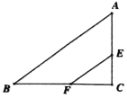
����Ŀ����ͼ����֪Rt��ABC�У���C=90����AC=6��BC=8����E��F�ֱ��DZ�AC��BC�ϵĶ���,��EF//AB����C����EF�ĶԳƵ�Dǡ��������ABC���ڽ�ƽ�����ϣ���CD��Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
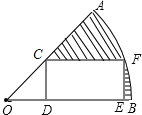
����Ŀ����ͼ���ڰ뾶Ϊ![]() ��Բ�Ľǵ���45��������AOB�ڲ���һ������CDEF��ʹ��C��OA�ϣ���D��E��OB�ϣ���F�ڻ�AB�ϣ���DE��2CD����
��Բ�Ľǵ���45��������AOB�ڲ���һ������CDEF��ʹ��C��OA�ϣ���D��E��OB�ϣ���F�ڻ�AB�ϣ���DE��2CD����
��1����AB�ij��ǣ������������________��
��2��ͼ����Ӱ���ֵ����Ϊ�������������________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������о���ƶ�����ѽ��빥��Σ�ƶ�����Ŵ�ү��ij��λ�İ���£���һƬ�µظ������ֲ������ˮ����ݮ��������ʽ�������ۣ������۵�30���У���һ������20ǧ�ˣ�Ϊ��������������ȡ�˽��۴�ʩ���Ժ�ÿ���ǰһ�������4ǧ�ˣ���x����ۼ�ΪyԪ/ǧ�ˣ�y����x�ĺ�������ʽΪ![]() �ҵ�12����ۼ�Ϊ32Ԫ/ǧ�ˣ���26����ۼ�Ϊ25Ԫ/ǧ�ˣ���֪��ֲ������ݮ�ij�ľ��18Ԫ/ǧ�ˣ�ÿ���������WԪ������=�������멁�ɱ�����
�ҵ�12����ۼ�Ϊ32Ԫ/ǧ�ˣ���26����ۼ�Ϊ25Ԫ/ǧ�ˣ���֪��ֲ������ݮ�ij�ľ��18Ԫ/ǧ�ˣ�ÿ���������WԪ������=�������멁�ɱ�����
��1��m=�� ����n=�� ����
��2����������ݮ�ڼ���ʱ����������������������Ƕ��٣�
��3����������ݮ��30���У�����������870Ԫ�Ĺ��ж����죿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������
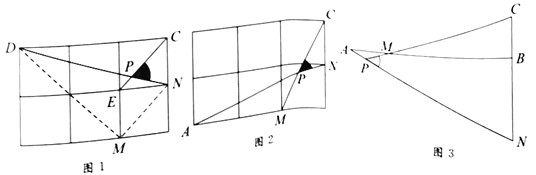
��ͼ1���ڱ߳�Ϊ1�������������У����Ӹ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() ��ֵ.
��ֵ.
��������
��һ����ǵ����Ǻ���ֵ������������Ҫ�ҳ����������һ��ֱ��������.�۲췢��������![]() ����ֱ���������У����dz�����������ƽ���ߵȷ��������������.�������Ӹ��
����ֱ���������У����dz�����������ƽ���ߵȷ��������������.�������Ӹ��![]() ��
��![]() ���ɵ�
���ɵ�![]() ����
����![]() ������
������![]() ����ô
����ô![]() �ͱ任����
�ͱ任����![]() .
.
������
��1��ֱ��д��ͼ1��![]() ��ֵΪ_________��
��ֵΪ_________��
��2����ͼ2���ڱ߳�Ϊ1�������������У�![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() ��ֵ��
��ֵ��
˼ά��չ
��3����ͼ3��![]() ��
��![]() ����
����![]() ��
��![]() �ϣ���
�ϣ���![]() ���ӳ�
���ӳ�![]() ��
��![]() ��ʹ
��ʹ![]() ������
������![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ����������������������
����������������������![]() �Ķ���.
�Ķ���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com