
【题目】如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F.
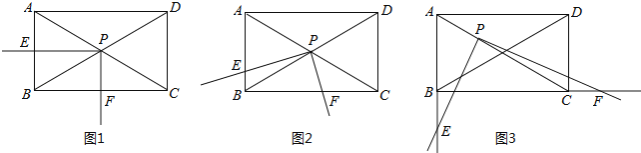
(1)当PE⊥AB,PF⊥BC时,如图1,则![]() 的值为 ;
的值为 ;
(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求![]() 的值;
的值;
(3)在(2)的基础上继续旋转,当60°<α<90°,且使AP:PC=1:2时,如图3,![]() 的值是否变化?证明你的结论.
的值是否变化?证明你的结论.
【答案】解:(1)![]() 。
。
(2)如答图1,过点P作PM⊥AB于点M,PN⊥BC于点N,则PM⊥PN。
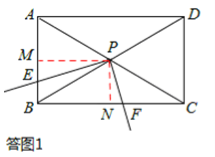
∵PM⊥PN,PE⊥PF,∴∠EPM=∠FPN。
又∵∠PME=∠PNF=90°,∴△PME∽△PNF。
∴![]() 。
。
由(1)知,![]() ,
,
∴![]() 。
。
(3)变化。证明如下:
如答图2,过点P作PM⊥AB于点M,PN⊥BC于点N,则PM⊥PN,PM∥BC,PN∥AB。
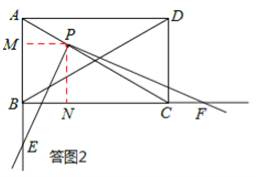
∵PM∥BC,PN∥AB,
∴∠APM=∠PCN,∠PAM=∠CPN。
∴△APM∽△PCN。
∴![]() ,得CN=2PM。
,得CN=2PM。
在Rt△PCN中,![]() ,
,
∴![]() 。
。
∵PM⊥PN,PE⊥PF,∴∠EPM=∠FPN。
又∵∠PME=∠PNF=90°,∴△PME∽△PNF。
∴![]() 。
。
∴![]() 的值发生变化
的值发生变化
【解析】
试题(1)证明△APE≌△PCF,得PE=CF;在Rt△PCF中,解直角三角形求得![]() 的值:
的值:
∵矩形ABCD,∴AB⊥BC,PA=PC。
∵PE⊥AB,BC⊥AB,∴PE∥BC。∴∠APE=∠PCF。
∵PF⊥BC,AB⊥BC,∴PF∥AB。∴∠PAE=∠CPF。
∵在△APE与△PCF中,∠PAE=∠CPF,PA=PC,∠APE=∠PCF,
∴△APE≌△PCF(ASA)。∴PE=CF。
在Rt△PCF中,![]() ,∴
,∴![]() 。
。
(2)如答图1所示,作辅助线,构造直角三角形,证明△PME∽△PNF,并利用(1)的结论,求得![]() 的值;
的值;
(3)如答图2所示,作辅助线,构造直角三角形,首先证明△APM∽△PCN,求得![]() ;然后证明△PME∽△PNF,从而由
;然后证明△PME∽△PNF,从而由![]() 求得
求得![]() 的值。与(1)(2)问相比较,
的值。与(1)(2)问相比较,![]() 的值发生了变化。
的值发生了变化。


科目:初中数学 来源: 题型:
【题目】用1块![]() 型钢板可制成2块
型钢板可制成2块![]() 型钢板和1块
型钢板和1块![]() 型钢板;用1块
型钢板;用1块![]() 型钢板可制成1块
型钢板可制成1块![]() 型钢板和3块
型钢板和3块![]() 型钢板.现准备购买
型钢板.现准备购买![]() 、
、![]() 型钢板共100块,并全部加工成
型钢板共100块,并全部加工成![]() 、
、![]() 型钢板.要求
型钢板.要求![]() 型钢板不少于120块,
型钢板不少于120块,![]() 型钢板不少于250块,设购买
型钢板不少于250块,设购买![]() 型钢板
型钢板![]() 块(
块(![]() 为整数)
为整数)
(1)求![]() 、
、![]() 型钢板的购买方案共有多少种?
型钢板的购买方案共有多少种?
(2)出售![]() 型钢板每块利润为100元,
型钢板每块利润为100元,![]() 型钢板每块利润为120元.若将
型钢板每块利润为120元.若将![]() 、
、![]() 型钢板全部出售,请你设计获利最大的购买方案,并求出最大利润.
型钢板全部出售,请你设计获利最大的购买方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
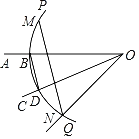
【题目】如图:已知锐角∠AOC,依次按照以下顺序操作画图:
(1)在射线OA上取一点B,以点O为圆心,OB长为半径作![]() ,交射线OC于点D,连接BD;
,交射线OC于点D,连接BD;
(2)分别以点B,D为圆心,BD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接ON,MN.
根据以上作图过程及所作图形可知下列结论:①OC平分∠AON;②MN∥BD;③MN=3BD;④若∠AOC=30°,则MN=![]() ON.其中正确结论的序号是_____.
ON.其中正确结论的序号是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小、质地完全相同,小李从布袋里随机取出一个小球,记下数字为x,小张在剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点Q的坐标(x,y).
(1)画树状图或列表,写出点Q所有可能的坐标;
(2)求点Q(x,y)在函数y=﹣x+5图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
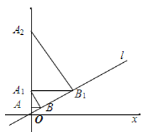
【题目】如图,已知直线l:y=![]() x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;……按此作法继续下去,则点A2020的坐标为______________.
x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;……按此作法继续下去,则点A2020的坐标为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将图中的A型、B型、C型矩形纸片分别放在3个盒子中,盒子的形状、大小、质地都相同,再将这3个盒子装入一只不透明的袋子中.
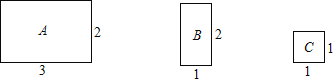
(1)搅匀后从中摸出1个盒子,求摸出的盒子中是![]() 型矩形纸片的概率;
型矩形纸片的概率;
(2)搅匀后先从中摸出1个盒子(不放回),再从余下的两个盒子中摸出一个盒子,求2次摸出的盒子的纸片能拼成一个新矩形的概率(不重叠无缝隙拼接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P为△ABC边上一动点,沿着A→C→B的路径行进,点P作PD⊥AB,垂足为D,设AD=x,△APD的面积为y,图2是y关于x的函数图象,则依据图中的数量关系计算△ACB的周长为( )
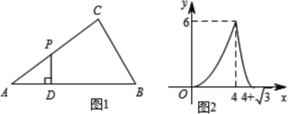

A.![]() B.15C.
B.15C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
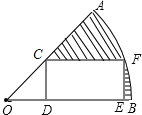
【题目】如图,在半径为![]() ,圆心角等于45°的扇形AOB内部作一个矩形CDEF,使点C在OA上,点D、E在OB上,点F在弧AB上,且DE=2CD,则:
,圆心角等于45°的扇形AOB内部作一个矩形CDEF,使点C在OA上,点D、E在OB上,点F在弧AB上,且DE=2CD,则:
(1)弧AB的长是(结果保留π)________;
(2)图中阴影部分的面积为(结果保留π)________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com