
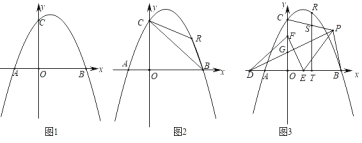
【题目】已知:在平面直角坐标系中,抛物线y=ax2﹣2ax+4(a<0)交x轴于点A、B,与y轴交于点C,AB=6.
(1)如图1,求抛物线的解析式;
(2)如图2,点R为第一象限的抛物线上一点,分别连接RB、RC,设△RBC的面积为s,点R的横坐标为t,求s与t的函数关系式;
(3)在(2)的条件下,如图3,点D在x轴的负半轴上,点F在y轴的正半轴上,点E为OB上一点,点P为第一象限内一点,连接PD、EF,PD交OC于点G,DG=EF,PD⊥EF,连接PE,∠PEF=2∠PDE,连接PB、PC,过点R作RT⊥OB于点T,交PC于点S,若点P在BT的垂直平分线上,OB﹣TS=![]() ,求点R的坐标.
,求点R的坐标.
【答案】(1)y=﹣![]() x2+x+4;(2)s=﹣t2+4t;(3)当a=1时,R(2,4),当a=
x2+x+4;(2)s=﹣t2+4t;(3)当a=1时,R(2,4),当a=![]() 时,R(
时,R(![]() ,
,![]() ).
).
【解析】
(1)由题意可求A(-2,0),B(4,0),将A点代入y=ax2-2ax+4,即可求a的值;
(2)设R(t,﹣![]() t2+t+4),过点R作x、y轴的垂线,垂足分别为R',R',可得四边形RR'OR'是矩形,求出S△OCR=
t2+t+4),过点R作x、y轴的垂线,垂足分别为R',R',可得四边形RR'OR'是矩形,求出S△OCR=![]() OCRR'=
OCRR'=![]() ×4t=2t,S△ORB=
×4t=2t,S△ORB=![]() OBRR'=
OBRR'=![]() ×4(﹣
×4(﹣![]() t2+t+4)=﹣t2+2t+8,则有S△RBC=S△ORB+S△OCR﹣S△OBC=﹣t2+2t+8+2t﹣
t2+t+4)=﹣t2+2t+8,则有S△RBC=S△ORB+S△OCR﹣S△OBC=﹣t2+2t+8+2t﹣![]() ×4×4=﹣t2+4t;
×4×4=﹣t2+4t;
(3)设EF、PD交于点G',连EG,可证明OP是EG的垂直平分线,过P作KP⊥x轴于K,PW⊥y轴于W,交RT于点H,则四边形PWOK是正方形,设OT=2a,则TK=KB=CW=2﹣a,HT=OK=PW=2+a,可求HS=TS﹣HT=![]() ﹣(2+a)=
﹣(2+a)=![]() ﹣a,又由tan∠HPS=
﹣a,又由tan∠HPS=![]() ,可得
,可得 ,则a=1或a=
,则a=1或a=![]() ,即可求R得坐标.
,即可求R得坐标.
解:(1)∵抛物线的对称轴为x=1,AB=6,
∴A(﹣2,0),B(4,0),
将点A代入y=ax2﹣2ax+4,则有0=4a+4a+4,
∴a=﹣![]() ,
,
∴y=﹣![]() x2+x+4;
x2+x+4;
(2)
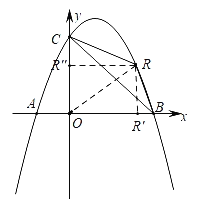
设R(t,﹣![]() t2+t+4),
t2+t+4),
过点R作x、y轴的垂线,垂足分别为R',R',
则∠RR'O=∠RR'O=∠R'OR'=90°,
∴四边形RR'OR'是矩形,
∴RR'=OR'=t,OR'=RR'=﹣![]() t2+t+4,
t2+t+4,
∴S△OCR=![]() OCRR'=
OCRR'=![]() ×4t=2t,
×4t=2t,
S△ORB=![]() OBRR'=
OBRR'=![]() ×4(﹣
×4(﹣![]() t2+t+4)=﹣t2+2t+8,
t2+t+4)=﹣t2+2t+8,
∴S△RBC=S△ORB+S△OCR﹣S△OBC=﹣t2+2t+8+2t﹣![]() ×4×4=﹣t2+4t;
×4×4=﹣t2+4t;
(3)
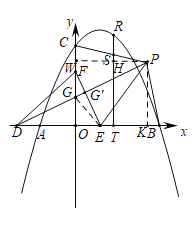
设EF、PD交于点G',连EG,
∵PD⊥EF,
∴∠FG'G=∠DG'E=90°=∠DOG,
∴∠OFE=∠GDO,
∵∠DGO=∠FOE=90°,EF=DG,
∴OP是EG的垂直平分线,
∴OP平分∠COB,
过P作KP⊥x轴于K,PW⊥y轴于W,交RT于点H,
则PW=PK,∠PWO=∠PKO=∠WOK=90°,
∴四边形PWOK是正方形,
∴WO=OK,
∵OC=OB=4,
∴CW=KB,
∵P在BT垂直平分线上,
∴PT=PB,
∴TK=KB=CW,
设OT=2a,则TK=KB=CW=2﹣a,
HT=OK=PW=2+a,
∵OB﹣TS=![]() ,
,
∴HS=TS﹣HT=![]() ﹣(2+a)=
﹣(2+a)=![]() ﹣a,
﹣a,
∵tan∠HPS=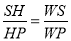 ,
,
∴ ,
,
∴a=1或a=![]() ,
,
当a=1时,OT=2,∴R(2,4),
当a=![]() 时,OT=
时,OT=![]() ,∴R(
,∴R(![]() ,
,![]() )
)
综上,点R的坐标是(2,4),(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
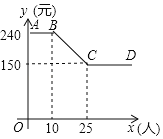
【题目】某公司组织员工到附近的景点旅游,根据旅行社提供的收费方案,绘制了如图所示的图象,图中折线ABCD表示人均收费y(元)与参加旅游的人数x(人)之间的函数关系.
(1)当参加旅游的人数不超过10人时,人均收费为 元;
(2)如果该公司支付给旅行社3600元,那么参加这次旅游的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据规定,我市将垃圾分为了四类:可回收垃圾、餐厨垃圾、有害垃圾和其他垃圾.现有投放这四类垃圾的垃圾桶各1个,若将用不透明垃圾袋分类打包好的两袋不同垃圾随机投人进两个不同的垃圾桶,投放正确的概率是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于平面直角坐标系![]() 中的线段
中的线段![]() 和点
和点![]() ,在
,在![]() 中,当
中,当![]() 边上的高为2时,称
边上的高为2时,称![]() 为
为![]() 的“等高点”,称此时
的“等高点”,称此时![]() 为
为![]() 的“等高距离”.
的“等高距离”.
(1)若点![]() 的坐标为(1,2),点
的坐标为(1,2),点![]() 的坐标为(4,2),则在点
的坐标为(4,2),则在点![]() (1,0),
(1,0),![]() (
(![]() ,4),
,4),![]() (0,3)中,
(0,3)中,![]() 的“等高点”是点___;
的“等高点”是点___;
(2)若![]() (0,0),
(0,0),![]() =2,当
=2,当![]() 的“等高点”在
的“等高点”在![]() 轴正半轴上且“等高距离”最小时,点
轴正半轴上且“等高距离”最小时,点![]() 的坐标是__.
的坐标是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
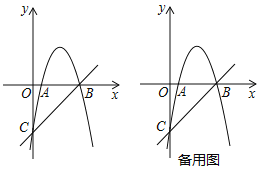
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() .直线
.直线![]() 经过点
经过点![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)过点![]() 的直线交直线
的直线交直线![]() 于点
于点![]() .
.
①当![]() 时,过抛物线上一动点
时,过抛物线上一动点![]() (不与点
(不与点![]() ,
,![]() 重合),作直线
重合),作直线![]() 的平行线交直线
的平行线交直线![]() 于点
于点![]() ,若以点
,若以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形,求点
为顶点的四边形是平行四边形,求点![]() 的横坐标;
的横坐标;
②连接![]() ,当直线
,当直线![]() 与直线
与直线![]() 的夹角等于
的夹角等于![]() 的
的![]() 倍时,请直接写出点
倍时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
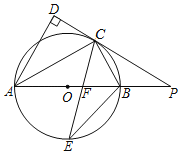
【题目】如图,AB 是⊙O的直径,∠DAB的角平分线AC交⊙O于点C,过点C作CD⊥AD于D,AB的延长线与DC的延长线相交于点P,∠ACB的角平分线CE交AB于点F、交⊙O于E.
(1)求证:PC与⊙O相切;
(2)求证:PC=PF;
(3)若AC=8,tan∠ABC=![]() ,求线段BE的长.
,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E是边BC上一点,连接AE,过点E作EM⊥AE,交对角线AC于点M,过点M作MN⊥AB,垂足为N,连接NE.
(1)求证:AE=![]() NE+ME;
NE+ME;
(2)如图2,延长EM至点F,使EF=EA,连接AF,过点F作FH⊥DC,垂足为H.
猜想CH与FH存在的数量关系,并证明你的结论;
(3)在(2)的条件下,若点G是AF的中点,连接GH.当GH=CH时,直接写出GH与AC之间存在的数量关系.
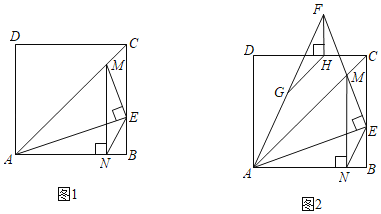
查看答案和解析>>
科目:初中数学 来源: 题型:
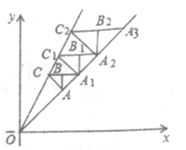
【题目】如图,在平面直角坐标系第一象限内,直线![]() 与直线
与直线![]() 的内部作等腰
的内部作等腰![]() ,使
,使![]() ,边
,边![]() 轴,
轴,![]() 轴,
轴,![]() 在直线
在直线![]() 上,点C在直线
上,点C在直线![]() 上,CB的延长线交直线
上,CB的延长线交直线![]() 于点
于点![]() ,作等腰
,作等腰![]() ,使
,使![]() 轴,
轴,![]() 轴,点
轴,点![]() 在直线
在直线![]() 上,按此规律,则等腰
上,按此规律,则等腰![]() 的腰长为_______.
的腰长为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com