
【题目】如图1,在正方形ABCD中,点E是边BC上一点,连接AE,过点E作EM⊥AE,交对角线AC于点M,过点M作MN⊥AB,垂足为N,连接NE.
(1)求证:AE=![]() NE+ME;
NE+ME;
(2)如图2,延长EM至点F,使EF=EA,连接AF,过点F作FH⊥DC,垂足为H.
猜想CH与FH存在的数量关系,并证明你的结论;
(3)在(2)的条件下,若点G是AF的中点,连接GH.当GH=CH时,直接写出GH与AC之间存在的数量关系.
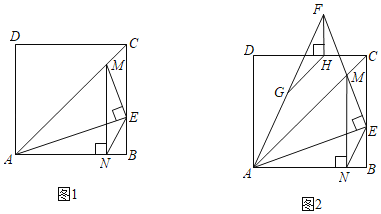
【答案】(1)见解析;(2)![]() ,见解析;(3)
,见解析;(3)![]()
【解析】
(1)如图1,过点N作NK⊥NE,交AE于点K.再证明△ANK≌△MNE得到,AK=ME,NK=NE,再根据正方形的性质即可证明;
(2)过点F作FP⊥BC,交BC的延长线于点P.可得∠P=∠PCH=∠CHF=90°,即四边形PCHF是矩形.再证明△ABE≌△EPF,可得BE=PF,AB=EP.即CP=BE=PF.可以说明矩形PCHF是正方形即可说明理由;
(3)延长FH交AC于点Q,由中位线定理可得出AQ=2GH,由等腰直角三角形的性质可得出CQ=![]() GH即可.
GH即可.
(1)证明:如图1,过点N作NK⊥NE,交AE于点K.
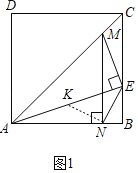
∴∠KNE=90°.
∵MN⊥AB,
∴∠MNA=90°.
∴∠ANK=∠MNE.
∵ME⊥AE,
∴∠AEM=∠ANM=90°.
∴∠NAK=∠NME.
∵四边形ABCD是正方形,∠ANM=90°.
∴∠MAN=∠NMA=45°.
∴AN=MN.
在△ANK和△MNE中,
 ,
,
∴△ANK≌△MNE(ASA).
∴AK=ME,NK=NE.
∴KE=![]() NE.
NE.
∴AE=AK+KE=ME+![]() NE.
NE.
(2)解:CH=FH,理由如下:
如图2,过点F作FP⊥BC,交BC的延长线于点P.
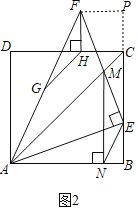
∴∠P=90°.
∵∠BAE+∠AEB=∠FEP+∠AEB=90°,
∴∠BAE=∠FEP.
∵四边形ABCD是正方形,
∴∠B=∠BCD=∠PCD=90°,AB=BC.
∵FH⊥CD,
∴∠FHC=90°.
∴∠P=∠PCH=∠CHF=90°.
∴四边形PCHF是矩形.
在△ABE和△EPF中,
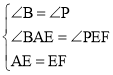 ,
,
∴△ABE≌△EPF(AAS).
∴BE=PF,AB=EP.
∵AB=BC,
∴EP=BC.
∴CP=BE=PF.
∴矩形PCHF是正方形.
∴FH=CH.
(3)AC=![]() GH,理由如下:
GH,理由如下:
如图3,延长FH交AC于点Q,
在正方形ABCD中,∠ACD=45°,
∵∠FHC=90°,
∴∠HQC=∠HCQ=45°,
∴CH=HQ,CQ=![]() CH,
CH,
∵CH=FH,
∴HQ=FH,
∵G是AF的中点,
∴GH=![]() AQ,
AQ,
又∵GH=CH,
∴CQ=![]() GH,
GH,
∴AC=AQ+CQ=2GH+![]() GH=(2+
GH=(2+![]() )GH.
)GH.


科目:初中数学 来源: 题型:
【题目】随着时代的不断发展,新颖的网络购进逐渐融入到人们的生活中,“拼一拼”电商平台上提供了一种拼团购买方式,当拼团(单数不超过15单)成功后商家将会让利一定的额度给予顾客实惠.现在某商家准备出手一种每件成本25元/件的新产品,经市场调研发现,单价y(单位:元)、日销售量m(单位:件)与拼单数x(单位:单)之间存在着如表的数量关系:
拼单数x(单位:单) | 2 | 4 | 8 | 12 |
单价y(单位:元) | 34.50 | 34.00 | 33.00 | 32.00 |
日销售量m(单位:件) | 68 | 76 | 92 | 108 |
请根据以上提供的信息解决下列问题:
(1)请直接写出单价y和日销售量m分别与拼单数x之间的一次函数关系式;
(2)拼单数设置为多少单时的日销售利润最大,最大的销售利润是多少?
(3)在实际销售过程中,厂家希望能有更多的商品出售,因此对电商每销售一件商品厂家就给予电商补助a元(a≤2),那么电商在获得补助之日后日销售利润能够随单数x的增大而增大,那么a的取值范围是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,抛物线y=ax2﹣2ax+4(a<0)交x轴于点A、B,与y轴交于点C,AB=6.
(1)如图1,求抛物线的解析式;
(2)如图2,点R为第一象限的抛物线上一点,分别连接RB、RC,设△RBC的面积为s,点R的横坐标为t,求s与t的函数关系式;
(3)在(2)的条件下,如图3,点D在x轴的负半轴上,点F在y轴的正半轴上,点E为OB上一点,点P为第一象限内一点,连接PD、EF,PD交OC于点G,DG=EF,PD⊥EF,连接PE,∠PEF=2∠PDE,连接PB、PC,过点R作RT⊥OB于点T,交PC于点S,若点P在BT的垂直平分线上,OB﹣TS=![]() ,求点R的坐标.
,求点R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,AD与BC相交于点E,AF平分∠BAD,交BC于点F,交CD的延长线于点G.

(1)若∠G=29°,求∠ADC的度数;
(2)若点F是BC的中点,求证:AB=AD+CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为推动“时刻听党话 永远跟党走”校园主题教育活动,计划开展四项活动:A:党史演讲比赛,B:党史手抄报比赛,C:党史知识竞赛,D:红色歌咏比赛.校团委对学生最喜欢的一项活动进行调查,随机抽取了部分学生,并将调查结果绘制成图1,图2两幅不完整的统计图.请结合图中信息解答下列问题:
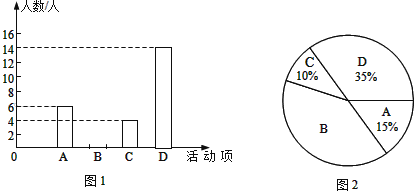
(1)本次共调查了 名学生;
(2)将图1的统计图补充完整;
(3)已知在被调查的最喜欢“党史知识竞赛”项目的4个学生中只有1名女生,现从这4名学生中任意抽取2名学生参加该项目比赛,请用画树状图或列表的方法,求出恰好抽到一名男生一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个芭蕾舞团演员的身高(单位:cm)如下表:
甲 | 164 | 164 | 165 | 165 | 166 | 166 | 167 | 167 |
乙 | 163 | 163 | 165 | 165 | 166 | 166 | 168 | 168 |
两组芭蕾舞团演员身高的方差较小的是______.(填“甲”或“乙”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.掷一枚质地均匀的正方体骰子,骰子停止转动后,5点朝上是必然事件
B.审查书稿中有哪些学科性错误适合用抽样调查法
C.甲乙两人在相同条件下各射击10次,他们的成绩的平均数相同,方差分别是![]() =0.4,
=0.4,![]() =0.6,则甲的射击成绩较稳定
=0.6,则甲的射击成绩较稳定
D.掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当白色小正方形个数按![]() 等于1,2,3,…时的某种规律增加时,由白色小正方形和黑色小正方形组成的图形分别如图所示,则第
等于1,2,3,…时的某种规律增加时,由白色小正方形和黑色小正方形组成的图形分别如图所示,则第![]() 个图形中白色小正方形和黑色小正方形的个数总和等于______.(用
个图形中白色小正方形和黑色小正方形的个数总和等于______.(用![]() 表示,
表示,![]() 是正整数)
是正整数)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com