
【题目】当白色小正方形个数按![]() 等于1,2,3,…时的某种规律增加时,由白色小正方形和黑色小正方形组成的图形分别如图所示,则第
等于1,2,3,…时的某种规律增加时,由白色小正方形和黑色小正方形组成的图形分别如图所示,则第![]() 个图形中白色小正方形和黑色小正方形的个数总和等于______.(用
个图形中白色小正方形和黑色小正方形的个数总和等于______.(用![]() 表示,
表示,![]() 是正整数)
是正整数)

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E是边BC上一点,连接AE,过点E作EM⊥AE,交对角线AC于点M,过点M作MN⊥AB,垂足为N,连接NE.
(1)求证:AE=![]() NE+ME;
NE+ME;
(2)如图2,延长EM至点F,使EF=EA,连接AF,过点F作FH⊥DC,垂足为H.
猜想CH与FH存在的数量关系,并证明你的结论;
(3)在(2)的条件下,若点G是AF的中点,连接GH.当GH=CH时,直接写出GH与AC之间存在的数量关系.
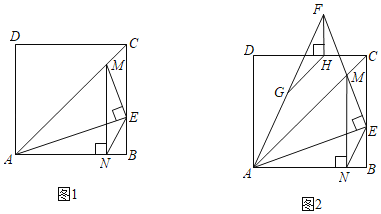
查看答案和解析>>
科目:初中数学 来源: 题型:
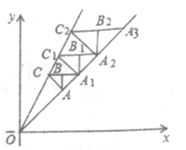
【题目】如图,在平面直角坐标系第一象限内,直线![]() 与直线
与直线![]() 的内部作等腰
的内部作等腰![]() ,使
,使![]() ,边
,边![]() 轴,
轴,![]() 轴,
轴,![]() 在直线
在直线![]() 上,点C在直线
上,点C在直线![]() 上,CB的延长线交直线
上,CB的延长线交直线![]() 于点
于点![]() ,作等腰
,作等腰![]() ,使
,使![]() 轴,
轴,![]() 轴,点
轴,点![]() 在直线
在直线![]() 上,按此规律,则等腰
上,按此规律,则等腰![]() 的腰长为_______.
的腰长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[阅读理解]
当![]() 且
且![]() 时,因为
时,因为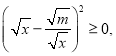 所以
所以![]() 从而
从而![]() (当且仅当
(当且仅当![]() 时取等号).由此可知,在
时取等号).由此可知,在![]() 且
且![]() 的条件下,当
的条件下,当![]() 时,代数式
时,代数式![]() 有最小值为
有最小值为![]() .
.
[实践应用]
(1)在![]() 的条件下,当
的条件下,当![]() 时,
时,![]() 有最小值,且最小值为 ;
有最小值,且最小值为 ;
(2)设![]() ,求
,求![]() 的最小值,并指出当
的最小值,并指出当![]() 取得该最小值时对应的
取得该最小值时对应的![]() 的值;
的值;
[拓展延伸]
在平面直角坐标系中,点![]() 点
点![]() .点
.点![]() 是函数
是函数![]() 在第一象限内图象上的一个动点,过
在第一象限内图象上的一个动点,过![]() 点作
点作![]() 垂直于
垂直于![]() 轴,
轴,![]() 垂直于
垂直于![]() 轴,垂足分别为点
轴,垂足分别为点![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() .
.

(3)求![]() 和
和![]() 之间的函数关系式:
之间的函数关系式:
(4)试判断当![]() 的值最小时,四边形
的值最小时,四边形![]() 是何特殊四边形,并说明理由.
是何特殊四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某开发商原计划对楼盘新房以每平方米4000元的销售价对外销售.现为了加快资金周转,对销售价经过两次下调后,决定在开盘之日以每平方米3240元的销售价进行促销.
(1)求销售价平均每次下调的百分率;
(2)开盘之日,开发商又给予以下两种优惠方案以供选择:方案①一次性送装修费每平方米50元;方案②打9.8折销售.张先生要购买一套100平方米的住房,试问哪种方案更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人开车从家出发去植物园游玩,设汽车行驶的路程为S(千米),所用时间为t(分),S与t之间的函数关系如图所示.若他早上8点从家出发,汽车在途中停车加油一次,则下列描述中,不正确的是( )
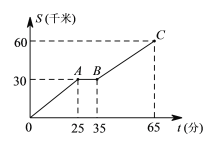
A.汽车行驶到一半路程时,停车加油用时10分钟
B.汽车一共行驶了60千米的路程,上午9点5分到达植物园
C.加油后汽车行驶的速度为60千米/时
D.加油后汽车行驶的速度比加油前汽车行驶的速度快
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AE平分∠BAC交BC于点E,D是AB边上一动点,连接CD交AE于点P,连接BP.已知AB =6cm,设B,D两点间的距离为xcm,B,P两点间的距离为y1cm,A,P两点间的距离为y2cm.
小明根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
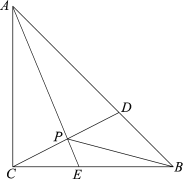
下面是小明的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,![]() 与x的几组对应值:
与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 2.49 | 2.64 | 2.88 | 3.25 | 3.80 | 4.65 | 6.00 |
y2/cm | 4.59 | 4.24 | 3.80 | 3.25 | 2.51 | 0.00 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,![]() ),并画出函数y1,
),并画出函数y1,![]() 的图象;
的图象;
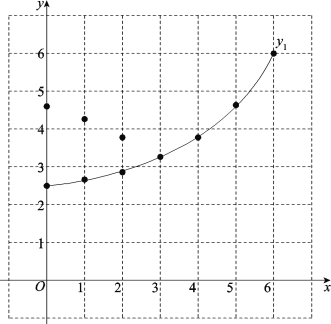
(3)结合函数图象,回答下列问题:
①当AP=2BD时,AP的长度约为 cm;
②当BP平分∠ABC时,BD的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB=2,AD=4,对角线AC,BD相交于点O,且E,F,G,H分别是AO,BO,CO,DO的中点,则下列说法正确的是( )
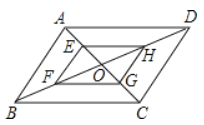
A.EH=HGB.四边形EFGH是平行四边形
C.AC⊥BDD.![]() 的面积是
的面积是![]() 的面积的2倍
的面积的2倍
查看答案和解析>>
科目:初中数学 来源: 题型:
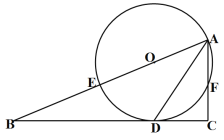
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A、D的⊙O分别交边AB、AC于点E、F.
(1)求证:BC是⊙O的切线;
(2)若BE=16,sinB=![]() ,求AF的长.
,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com