
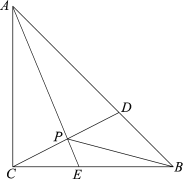
【题目】如图,在△ABC中,AE平分∠BAC交BC于点E,D是AB边上一动点,连接CD交AE于点P,连接BP.已知AB =6cm,设B,D两点间的距离为xcm,B,P两点间的距离为y1cm,A,P两点间的距离为y2cm.
小明根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,![]() 与x的几组对应值:
与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 2.49 | 2.64 | 2.88 | 3.25 | 3.80 | 4.65 | 6.00 |
y2/cm | 4.59 | 4.24 | 3.80 | 3.25 | 2.51 | 0.00 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,![]() ),并画出函数y1,
),并画出函数y1,![]() 的图象;
的图象;
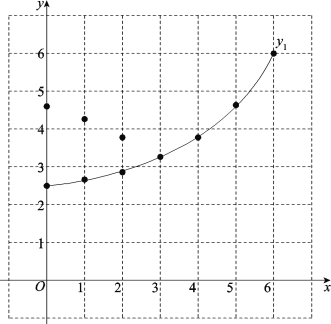
(3)结合函数图象,回答下列问题:
①当AP=2BD时,AP的长度约为 cm;
②当BP平分∠ABC时,BD的长度约为 cm.
【答案】(1)1.5;(2)详见解析;(3)答案不唯一,如:①3.86;②3
【解析】
(1)用光滑的曲线连接y2图象现有的点,在图象上,测量出x=5时,y的值即可;
(2)描点连线即可绘出函数图象;
(3)①当AP=2BD时,即y2=2x,在图象上画出直线y=2x,该图象与y2的交点即为所求;
②从表格数据看,当x=3时,y1=y2=3.25,故当BP平分∠ABC时,此时点P是△ABC的内心,故点D在AB的中点,即可求解.
解:(1)根据测量结果得到:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 2.49 | 2.64 | 2.88 | 3.25 | 3.80 | 4.65 | 6.00 |
y2/cm | 4.59 | 4.24 | 3.80 | 3.25 | 2.51 | 1.5 | 0.00 |
(2)画出函数![]() 的图象;
的图象;
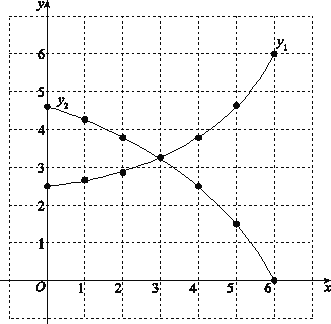
(3)①当AP=2BD时,即y2=2x,
在图象上画出直线y=2x,该图象与y2的交点即为所求,即图中空心点所示,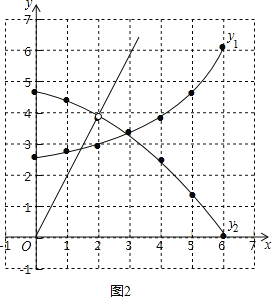
空心点的纵坐标为3.86,
②从表格数据看,当x=3时,y1=y2=3.25,
即点D在AB中点时,y1=y2,即此时点P在AB的中垂线上,则点C在AB的中垂线上,则△ABC为等腰三角形,
故当BP平分∠ABC时,此时点P是△ABC的内心,故点D在AB的中点,
![]()
故答案可以为:①3.86;②3.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两个芭蕾舞团演员的身高(单位:cm)如下表:
甲 | 164 | 164 | 165 | 165 | 166 | 166 | 167 | 167 |
乙 | 163 | 163 | 165 | 165 | 166 | 166 | 168 | 168 |
两组芭蕾舞团演员身高的方差较小的是______.(填“甲”或“乙”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,将直角的顶点E放在正方形ABCD的对角线AC上,使角的一边交CD于点F,另一边交CB或其延长线于点G,求![]() 的值;
的值;
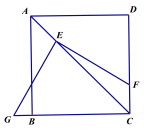
(2)如图,将(1)中的“正方形ABCD”改成“矩形ABCD”,其他条件不变.若AB=m,BC=n,试求![]() 的值;
的值;
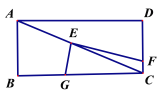
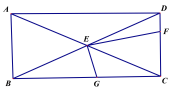
(3)如图,将直角顶点E放在矩形ABCD的对角线交点,EF、EG分别交CD与CB于点F、G,且EC平分∠FEG.若AB=2,BC=4,直接写出EG、EF 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当白色小正方形个数按![]() 等于1,2,3,…时的某种规律增加时,由白色小正方形和黑色小正方形组成的图形分别如图所示,则第
等于1,2,3,…时的某种规律增加时,由白色小正方形和黑色小正方形组成的图形分别如图所示,则第![]() 个图形中白色小正方形和黑色小正方形的个数总和等于______.(用
个图形中白色小正方形和黑色小正方形的个数总和等于______.(用![]() 表示,
表示,![]() 是正整数)
是正整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某调查机构对某地互联网行业从业情况进行调查统计,得到当地互联网行业从业人员年龄分布统计图和当地90后从事互联网行业岗位分布统计图:
互联网行业从业人员年龄分布统计图 90后从事互联网行业岗位分布图
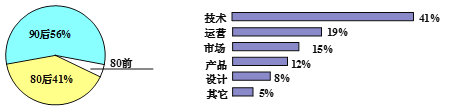
对于以下四种说法,你认为正确的是_____ (写出全部正确说法的序号).
①在当地互联网行业从业人员中,90后人数占总人数的一半以上
②在当地互联网行业从业人员中,80前人数占总人数的13%
③在当地互联网行业中,从事技术岗位的90后人数超过总人数的20%
④在当地互联网行业中,从事设计岗位的90后人数比80前人数少
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人开车从家出发去植物园游玩,设汽车行驶的路程为S(千米),所用时间为t(分),S与t之间的函数关系如图所示.若他早上8点从家出发,汽车在途中停车加油一次,则下列描述中,不正确的是( )
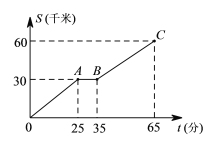
A.汽车行驶到一半路程时,停车加油用时10分钟
B.汽车一共行驶了60千米的路程,上午9点5分到达植物园
C.加油后汽车行驶的速度为60千米/时
D.加油后汽车行驶的速度比加油前汽车行驶的速度快
查看答案和解析>>
科目:初中数学 来源: 题型:
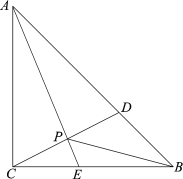
【题目】如图,在△ABC中,AE平分∠BAC交BC于点E,D是AB边上一动点,连接CD交AE于点P,连接BP.已知AB =6cm,设B,D两点间的距离为xcm,B,P两点间的距离为y1cm,A,P两点间的距离为y2cm.
小明根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
下面是小明的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,![]() 与x的几组对应值:
与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 2.49 | 2.64 | 2.88 | 3.25 | 3.80 | 4.65 | 6.00 |
y2/cm | 4.59 | 4.24 | 3.80 | 3.25 | 2.51 | 0.00 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,![]() ),并画出函数y1,
),并画出函数y1,![]() 的图象;
的图象;

(3)结合函数图象,回答下列问题:
①当AP=2BD时,AP的长度约为 cm;
②当BP平分∠ABC时,BD的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某制药厂需要紧急生产一批能有效缓解“新冠肺炎”的药品,要求必须在12天(含12天)内完成.为了加快生产,车间采取工人加班,机器不停的生产方式,这样每天药品的产量![]() (吨)是时间
(吨)是时间![]() (天)的一次函数,且满足如下表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本
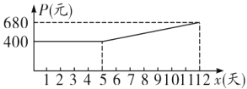
(天)的一次函数,且满足如下表中所对应的数量关系.由于机器负荷运转产生损耗,平均生产每吨药品的成本![]() (元)与时间
(元)与时间![]() (天)的关系满足如图所示的函数图象.
(天)的关系满足如图所示的函数图象.
时间 | 2 | 4 |
每天产量 | 24 | 28 |
(1)求药品每天的产量![]() (吨)与时间
(吨)与时间![]() (天)之间的函数关系式;
(天)之间的函数关系式;
(2)当![]() 时,直接写出
时,直接写出![]() (元)与时间
(元)与时间![]() (天)的函数关系是
(天)的函数关系是![]() ;
;
(3)若这批药品的价格为1400元/吨,每天的利润设为![]() 元,求哪一天的利润最高,最高利润是多少?(利润
元,求哪一天的利润最高,最高利润是多少?(利润![]() 售价
售价![]() 成本)
成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 上一动点,过
上一动点,过![]() 作
作![]() 的垂线交
的垂线交![]() 于
于![]() ,将
,将![]() 折叠得到
折叠得到![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
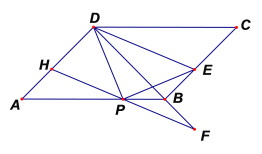
(1)求证:![]() ;
;
(2)当![]() 时,证明
时,证明![]() 是等腰三角形;
是等腰三角形;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com