
【题目】某校组织学生开展义务植树活动,在活动结束后随机调查了40名学生每人植树的棵数,根据调查获取的样本数据,制作了条形统计图和扇形统计图.请根据相关信息,解答下列问题:
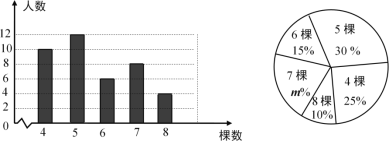
(1)扇形图中![]() 的值是_________;
的值是_________;
(2)求随机调查的40名学生每人植树棵数这组数据的平均数、众数和中位数;
(3)若本次活动九年级共有300名学生参加,估计植树超过6棵(不含6棵)的学生约有多少人.
【答案】(1)20;(2)平均数是5.6;众数是5;中位数是![]() ;(3)植树超过6棵(不含6棵)约有90人
;(3)植树超过6棵(不含6棵)约有90人
【解析】
(1)根据扇形统计图中的数据,即可得到m的值;
(2)根据条形统计图中的数据,即可得到这组数据的平均数、众数和中位数;
(3)根据扇形统计图中的数据,即可计算出植树超过6棵(不含6棵)的学生约有多少人.
解:(1))m%=1-25%-30%-15%-10%=20%,
即m的值是20.
故答案为:20;
(2)∵![]() ,
,
∴平均数是5.6;
∵5出现了12次,出现次数最多,
∴众数是5;
∵将这40个数据按从小到大顺序排列,中间的两个数都是5,
∴中位数是![]() .
.
(3)∵![]() ,
,
∴植树超过6棵(不含6棵)约有90人.


科目:初中数学 来源: 题型:
【题目】如图1,点![]() 是
是![]() 的内部一点,连接
的内部一点,连接![]() 、
、![]() 和
和![]() ,如果
,如果![]() 、
、![]() 和
和![]() 中有两个角相等,则称
中有两个角相等,则称![]() 是
是![]() 的“等心”.特别地,若这三个角都相等,则称
的“等心”.特别地,若这三个角都相等,则称![]() 是
是![]() 的“恒等心”.
的“恒等心”.
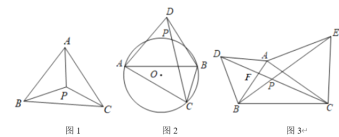
(1)在等边![]() 中,点
中,点![]() 是恒等心,
是恒等心,![]() ,则点
,则点![]() 到
到![]() 的距离是_______;
的距离是_______;
(2)如图2,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的外接圆外一点,连接
的外接圆外一点,连接![]() ,交
,交![]() 于点
于点![]() ,试判断
,试判断![]() 是不是
是不是![]() 的“等心”,并说明理由;
的“等心”,并说明理由;
(3)如图3,分别以锐角![]() 的边
的边![]() 、
、![]() 为边向外做等边
为边向外做等边![]() 和等边
和等边![]() ,
,![]() 和
和![]() 相交于点
相交于点![]() ,求证:点
,求证:点![]() 是
是![]() 的“恒等心”.
的“恒等心”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,AD与BC相交于点E,AF平分∠BAD,交BC于点F,交CD的延长线于点G.

(1)若∠G=29°,求∠ADC的度数;
(2)若点F是BC的中点,求证:AB=AD+CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个芭蕾舞团演员的身高(单位:cm)如下表:
甲 | 164 | 164 | 165 | 165 | 166 | 166 | 167 | 167 |
乙 | 163 | 163 | 165 | 165 | 166 | 166 | 168 | 168 |
两组芭蕾舞团演员身高的方差较小的是______.(填“甲”或“乙”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的点P和图形M,给出如下定义:Q为图形M上任意一点,如果
中的点P和图形M,给出如下定义:Q为图形M上任意一点,如果![]() 两点间的距离有最大值,那么称这个最大值为点P与图形M间的开距离,记作
两点间的距离有最大值,那么称这个最大值为点P与图形M间的开距离,记作![]() .已知直线
.已知直线![]() 与x轴交于点A,与y轴交于点B,
与x轴交于点A,与y轴交于点B,![]() 的半径为1.
的半径为1.
(1)若![]() ,
,
①求![]() 的值;
的值;
②若点C在直线![]() 上,求
上,求![]() 的最小值;
的最小值;
(2)以点A为中心,将线段![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,点E在线段
,点E在线段![]() 组成的图形上,若对于任意点E,总有
组成的图形上,若对于任意点E,总有![]() ,直接写出b的取值范围.
,直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.掷一枚质地均匀的正方体骰子,骰子停止转动后,5点朝上是必然事件
B.审查书稿中有哪些学科性错误适合用抽样调查法
C.甲乙两人在相同条件下各射击10次,他们的成绩的平均数相同,方差分别是![]() =0.4,
=0.4,![]() =0.6,则甲的射击成绩较稳定
=0.6,则甲的射击成绩较稳定
D.掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
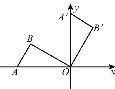
【题目】如图,将置于平面直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A'OB'.已知∠AOB=30°,∠B=90°,AB=1,则B'点的坐标为 ( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,将直角的顶点E放在正方形ABCD的对角线AC上,使角的一边交CD于点F,另一边交CB或其延长线于点G,求![]() 的值;
的值;
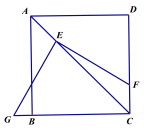
(2)如图,将(1)中的“正方形ABCD”改成“矩形ABCD”,其他条件不变.若AB=m,BC=n,试求![]() 的值;
的值;
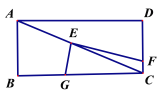
(3)如图,将直角顶点E放在矩形ABCD的对角线交点,EF、EG分别交CD与CB于点F、G,且EC平分∠FEG.若AB=2,BC=4,直接写出EG、EF 的长.
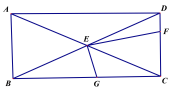
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AE平分∠BAC交BC于点E,D是AB边上一动点,连接CD交AE于点P,连接BP.已知AB =6cm,设B,D两点间的距离为xcm,B,P两点间的距离为y1cm,A,P两点间的距离为y2cm.
小明根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
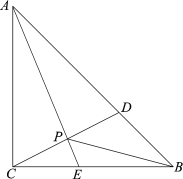
下面是小明的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,![]() 与x的几组对应值:
与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 2.49 | 2.64 | 2.88 | 3.25 | 3.80 | 4.65 | 6.00 |
y2/cm | 4.59 | 4.24 | 3.80 | 3.25 | 2.51 | 0.00 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,![]() ),并画出函数y1,
),并画出函数y1,![]() 的图象;
的图象;

(3)结合函数图象,回答下列问题:
①当AP=2BD时,AP的长度约为 cm;
②当BP平分∠ABC时,BD的长度约为 cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com