
【题目】抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴的一个交点
轴的一个交点![]() 在点
在点![]() 和
和![]() 之间,其部分图象如图所示,则以下结论:①
之间,其部分图象如图所示,则以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④方程以
;④方程以![]() 有两个的实根,其中正确的个数为( )
有两个的实根,其中正确的个数为( )
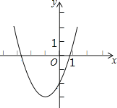
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】
抛物线开口向上a>0,对称轴在y轴左侧,b>0,抛物线和y轴负半轴相交,c<0,则abc<0,由抛物线与x轴有两个交点得到b2-4ac>0;有抛物线顶点坐标得到抛物线的对称轴为直线x=-1,则根据抛物线的对称性得抛物线与x轴的另一个交点在点(-3,0)和(-2,0)之间,所以当x=1时,y>0,则a+b+c>0;由抛物线的顶点为D(-1,-3)得a-b+c=-3,由抛物线的对称轴为直线![]() 得b=2a,所以a-c=3;根据二次函数的最值问题,当x=-1时,二次函数有最小值为-3,即b2-4ac=-12a,b2-4a(c+3)=b2-4ac-12a=-24a,所以说方程ax2+bx+c+3=0无实数根.
得b=2a,所以a-c=3;根据二次函数的最值问题,当x=-1时,二次函数有最小值为-3,即b2-4ac=-12a,b2-4a(c+3)=b2-4ac-12a=-24a,所以说方程ax2+bx+c+3=0无实数根.
∵抛物线开口向上,
∴a>0,
∵对称轴在y轴左侧,
∴b>0,
∵抛物线和y轴负半轴相交,
∴c<0,
∴abc<0,故①错误;
∵当x=1时,y>0,
∴y=a+b+c>0,故②错误;
∵抛物线的顶点为D(1,3)
∴ab+c=3,
∵抛物线的对称轴为直线![]() 得b=2a,
得b=2a,
把b=2a代入ab+c=3,得a2a+c=3,
∴ca=3,
∴ac=3,故③正确;
∵二次函数y=ax2+bx+c有最小值为3,
∴b24ac=12a,
∴方程ax2+bx+c+3=0的判别式△=b24a(c+3)=b24ac12a=0,
∴方程ax2+bx+c+3=0有两个相等的实数根,故④正确;
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() .
.
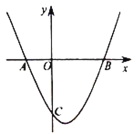
(1)求![]() 点坐标;
点坐标;
(2)若对于每一个给定的![]() 的值,它所对应的函数值都不小于
的值,它所对应的函数值都不小于![]() ,求
,求![]() 的取值范围.
的取值范围.
(3)直线![]() 经过点
经过点![]() .
.
①求直线和抛物线的解析式;
②设抛物线与![]() 轴的交点为
轴的交点为![]() ,过点
,过点![]() 作直线
作直线![]() 轴,将抛物线在
轴,将抛物线在![]() 轴左侧的部分沿直线
轴左侧的部分沿直线![]() 翻折,抛物线的其余部分保持不变,得到一个新图像,请你结合新图像回答:
翻折,抛物线的其余部分保持不变,得到一个新图像,请你结合新图像回答:
当直线![]() 与新图像只有一个公共点
与新图像只有一个公共点![]() 且
且![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
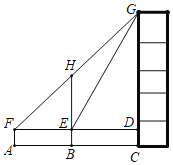
【题目】如图,某数学兴趣小组为测量一颗古树![]() 和教学楼
和教学楼![]() 的高,先在处用高15米的测角仪
的高,先在处用高15米的测角仪![]() 测得古树顶端
测得古树顶端![]() 的仰角
的仰角![]() 为45°,此时教学楼顶端
为45°,此时教学楼顶端![]() 恰好在视线
恰好在视线![]() 上,再向前走10米到达
上,再向前走10米到达![]() 处,又测得教学楼顶端
处,又测得教学楼顶端![]() 的仰角
的仰角![]() 为60°,点
为60°,点![]() 、
、![]() 、
、![]() 三点在同一水平线上.
三点在同一水平线上.
(1)求古树![]() 的高;
的高;
(2)求教学楼![]() 的高.(参考数据:
的高.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在标有平行四边形、矩形、菱形、正方形、等腰梯形、直角梯形的六张形状、大小完全相等的纸片中,连续抽取其中两张纸片,被抽中的(所对应的图形)恰好是轴对称的概率是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() 点
点![]() 在边
在边![]() 上(不与
上(不与![]() 重合),将矩形沿
重合),将矩形沿![]() 折叠,使点
折叠,使点![]() 分别落在点
分别落在点![]() 处有下列结论:
处有下列结论:
①![]() 与
与![]() 互余;
互余;
②若![]() 平分
平分![]() 则
则![]()
③若直线![]() 经过点
经过点![]() 则
则![]()
④若直线![]() 交边
交边![]()
![]() 分别于
分别于![]() 当
当![]() 为等腰三角形时,五边形
为等腰三角形时,五边形![]() 的周长为
的周长为![]() .其中正确结论的序号是_____________________.
.其中正确结论的序号是_____________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某开发商原计划对楼盘新房以每平方米4000元的销售价对外销售.现为了加快资金周转,对销售价经过两次下调后,决定在开盘之日以每平方米3240元的销售价进行促销.
(1)求销售价平均每次下调的百分率;
(2)开盘之日,开发商又给予以下两种优惠方案以供选择:方案①一次性送装修费每平方米50元;方案②打9.8折销售.张先生要购买一套100平方米的住房,试问哪种方案更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组要测量一栋五层居民楼CD的高度,该楼底层为车库,高2.5米;上面五层居住,每层高度相等,测角仪支架离地1.5米,在A处测得五楼顶部点D的仰角为60°,在B处测得四楼顶部点E的仰角为30°,AB=14米,求居民楼的高度.(精确到0.1米,参考数据:![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某调查机构对某地互联网行业从业情况进行调查统计,得到当地互联网行业从业人员年龄分布统计图和当地90后从事互联网行业岗位分布统计图:
互联网行业从业人员年龄分布统计图 90后从事互联网行业岗位分布图
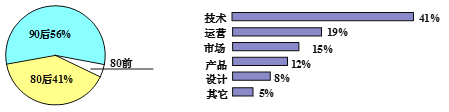
对于以下四种说法,你认为正确的是_____ (写出全部正确说法的序号).
①在当地互联网行业从业人员中,90后人数占总人数的一半以上
②在当地互联网行业从业人员中,80前人数占总人数的13%
③在当地互联网行业中,从事技术岗位的90后人数超过总人数的20%
④在当地互联网行业中,从事设计岗位的90后人数比80前人数少
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com